Chapter 10 Modelos Neurais
10.1 Veja uma Rede Neural em Funcionamento
Vamos entrar em http://playground.tensorflow.org/ e ver um rede neural em funcionamento.
knitr::include_url("http://playground.tensorflow.org/")10.2 Neurônio simples
Um neurônio artificial nada mais é do que um artefato de software que faz uma combinação linear das entradas e aplica um função de ativação como a função \(sign\), \(tanh\) ou \(relu\) para produzir uma saída.
\[ f(X) = sign( w_0 + w_1 x_1 + ... + w_n x_n ) \]
O treinamento do neurônio é feito ajustando-se os pesos \(w_n\) de acordo com o erro de predição obtido para se estimar a saída \(f(X) \cong y\).
\[ \min_{W} \sum || f(X)- y || \]
10.3 Redes neurais
Um único neurônio entretanto tem uma capacidade limitada de aprendizado. Por exemplo, ele não consegue aprender a função XOR.
Função \(XOR(X) \rightarrow y\):
X y
0 0 0
0 1 1
1 0 1
1 0 0Pois um único neurônio somente tem capacidade para fazer a separação de conjuntos linearmente separáveis.
Para resolver essa limitação podemos então trabalhar com múltiplos neurônios em camadas. As saídas dos neurônios de uma camada são então empregadas como entradas para a camada seguinte. As camadas entre a camada inicial de neurônios (de entrada) e a camada final (de saída) constitui as camadas ocultas da rede.
O treinamento da rede segue o mesmo princípio, embora mais complexo, ajustando os pesos \(w_n\) de acordo com o erro de predição obtido para se estimar a saída \(f(X) \cong y\).
\[ \min_{W} \sum || f(X)- y || \]
Chamamos esse aprendizado de backpropagation ou retropropagação.
10.4 Teorema da Aproximação Universal
Pode-se demonstrar (George Cybenko, 1989 e Kurt Hornik, 1991) que redes neurais de múltiplas camadas são aproximadores universais de funções o quê dá uma grande capacidade para os modelos neurais.
10.5 Deeplearning
Modelos deeplearning são baseados em modelos neurais exatamente como vimos, mas incluem a ideia de que um maior número de camadas fornece uma capacidade maior de representação dos dados. Embora as redes deeplearning não difiram essencialmente do modelo neural tradicional várias arquiteturas de rede (redes convolucionais, recorrentes etc.) foram desenvolvidas nos últimos anos aproveitando uma maior capacidade computacional antes não disponível.
Em geral as bibliotecas deeplearning, para buscar eficiência no treinamento e execução de redes profundas (até dezenas e centenas de camadas com milhares de neurônios) , implementam uma série de recursos como a representação dos dados por tensores, execução em árvore de cálculos e uso de gpu. Algumas das bibliotecas mais empregadas são TensorFlow/Keras, CNTK, PyTorch.
Para R empregaremos H2O como biblioteca de deeplearning.
nota: No momento que escrevemos este texto a integração do Python com bibliotecas Deeplearning parece mais facilitado que em R.
10.6 Modelos Neurais são sempre melhores que quaisquer outros modelos?
Não. Modelos neurais tem uma grande capacidade e os modelos deeplearning permitiram a solução de vários problemas que antes não podíamos resolver com modelos mais tradicionais. Carros autonômos, tradução automática de texto e speech, reconhecimento de imagens e pessoas são algumas de suas aplicações. Mas para muitos outros problemas a busca de um modelo para os dados depende essencialmente do dado em questão que, para alguns, modelos como uma árvore de decisão (random forest) ou outros modelos tradicionais ainda podem trazer uma resposta melhor. Além disso as redes neurais, por apresentarem um grande número de parâmetros (hyperprameters), nem sempre são fáceis de treinar.
10.7 Um Modelo Neural Simples em R
Modelos neurais podem ser empregados para implementar modelos Supervisionados e não Supervisionados, podemos usar para Classificação, Regressão não Linear, Clusterização e muitas outras tarefas. Aqui vamos nos ater a modelos Supervisionados para Classificação. Aqui empregamos a biblioteca neuralnet para classificação.
library("neuralnet")## Warning: package 'neuralnet' was built under R version 3.5.3# install.packages('ISLR')
library(ISLR)## Warning: package 'ISLR' was built under R version 3.5.3RNGversion('3.5.0')
set.seed(1984)
data = College
head(data)## Private Apps Accept Enroll Top10perc Top25perc
## Abilene Christian University Yes 1660 1232 721 23 52
## Adelphi University Yes 2186 1924 512 16 29
## Adrian College Yes 1428 1097 336 22 50
## Agnes Scott College Yes 417 349 137 60 89
## Alaska Pacific University Yes 193 146 55 16 44
## Albertson College Yes 587 479 158 38 62
## F.Undergrad P.Undergrad Outstate Room.Board Books
## Abilene Christian University 2885 537 7440 3300 450
## Adelphi University 2683 1227 12280 6450 750
## Adrian College 1036 99 11250 3750 400
## Agnes Scott College 510 63 12960 5450 450
## Alaska Pacific University 249 869 7560 4120 800
## Albertson College 678 41 13500 3335 500
## Personal PhD Terminal S.F.Ratio perc.alumni Expend
## Abilene Christian University 2200 70 78 18.1 12 7041
## Adelphi University 1500 29 30 12.2 16 10527
## Adrian College 1165 53 66 12.9 30 8735
## Agnes Scott College 875 92 97 7.7 37 19016
## Alaska Pacific University 1500 76 72 11.9 2 10922
## Albertson College 675 67 73 9.4 11 9727
## Grad.Rate
## Abilene Christian University 60
## Adelphi University 56
## Adrian College 54
## Agnes Scott College 59
## Alaska Pacific University 15
## Albertson College 55data_scaled = data
data_scaled[,2:18] = scale(data[,2:18])
L = sample(1:nrow(data),round(nrow(data)/3))
train = as.data.frame(data_scaled[-L,])
test = as.data.frame(data_scaled[L,])
# n = names(train)
# f <- as.formula(paste("Private ~", paste(n[!n %in% "Private"], collapse = " + ")))
f <- "Private ~ ."
net = neuralnet(f,data=train,hidden=c(5,3),linear.output=F)
plot(net)
predicted_data = predict(net,test[,2:18])
predicted_data = max.col(predicted_data)
predicted_data = levels(data$Private)[predicted_data]
cm = table(predicted_data,test$Private)
print(cm)##
## predicted_data No Yes
## No 59 16
## Yes 5 179cat('Accuracy : ', sum(diag(cm))/sum(cm)* 100, '%')## Accuracy : 91.89189 %10.8 Um modelo DeepLearning com H2O
Aqui um modelo de Deeplearning empregando a biblioteca H2o.
RNGversion('3.5.0')
set.seed(1984)
# install.packages('h2o)
library(h2o)## Warning: package 'h2o' was built under R version 3.5.3##
## ----------------------------------------------------------------------
##
## Your next step is to start H2O:
## > h2o.init()
##
## For H2O package documentation, ask for help:
## > ??h2o
##
## After starting H2O, you can use the Web UI at http://localhost:54321
## For more information visit http://docs.h2o.ai
##
## ----------------------------------------------------------------------##
## Attaching package: 'h2o'## The following objects are masked from 'package:stats':
##
## cor, sd, var## The following objects are masked from 'package:base':
##
## %*%, %in%, &&, ||, apply, as.factor, as.numeric, colnames,
## colnames<-, ifelse, is.character, is.factor, is.numeric, log,
## log10, log1p, log2, round, signif, trunc# install.packages('bit64')
# library(bit64) # for speed data.table
h2o.init()##
## H2O is not running yet, starting it now...## Warning in .h2o.startJar(ip = ip, port = port, name = name, nthreads = nthreads, : You have a 32-bit version of Java. H2O works best with 64-bit Java.
## Please download the latest Java SE JDK from the following URL:
## https://www.oracle.com/technetwork/java/javase/downloads/index.html##
## Note: In case of errors look at the following log files:
## C:\Users\rdeol\AppData\Local\Temp\Rtmp6X33kK\file64dc73bb45ae/h2o_rdeol_started_from_r.out
## C:\Users\rdeol\AppData\Local\Temp\Rtmp6X33kK\file64dc7d476dab/h2o_rdeol_started_from_r.err
##
##
## Starting H2O JVM and connecting: ... Connection successful!
##
## R is connected to the H2O cluster:
## H2O cluster uptime: 13 seconds 499 milliseconds
## H2O cluster timezone: America/Sao_Paulo
## H2O data parsing timezone: UTC
## H2O cluster version: 3.30.0.1
## H2O cluster version age: 7 months and 12 days !!!
## H2O cluster name: H2O_started_from_R_rdeol_rlj378
## H2O cluster total nodes: 1
## H2O cluster total memory: 0.97 GB
## H2O cluster total cores: 0
## H2O cluster allowed cores: 0
## H2O cluster healthy: TRUE
## H2O Connection ip: localhost
## H2O Connection port: 54321
## H2O Connection proxy: NA
## H2O Internal Security: FALSE
## H2O API Extensions: Amazon S3, Algos, AutoML, Core V3, TargetEncoder, Core V4
## R Version: R version 3.5.2 (2018-12-20)## Warning in h2o.clusterInfo():
## Your H2O cluster version is too old (7 months and 12 days)!
## Please download and install the latest version from http://h2o.ai/download/# c1=h2o.init(max_mem_size = "2G",
# nthreads = 2,
# ip = "localhost",
# port = 54321)
head(iris)## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosa
## 6 5.4 3.9 1.7 0.4 setosamodel = h2o.deeplearning(1:4,5, # input X,y
as.h2o(iris), # df input
epochs=100, # train limit
hidden=c(4,16,4)) # network##
|
| | 0%
|
|======================================================================| 100%
##
|
| | 0%
|
|======================================================================| 100%summary(model)## Model Details:
## ==============
##
## H2OMultinomialModel: deeplearning
## Model Key: DeepLearning_model_R_1605535249587_1
## Status of Neuron Layers: predicting Species, 3-class classification, multinomial distribution, CrossEntropy loss, 183 weights/biases, 6,6 KB, 15.000 training samples, mini-batch size 1
## layer units type dropout l1 l2 mean_rate rate_rms momentum
## 1 1 4 Input 0.00 % NA NA NA NA NA
## 2 2 4 Rectifier 0.00 % 0.000000 0.000000 0.000854 0.000387 0.000000
## 3 3 16 Rectifier 0.00 % 0.000000 0.000000 0.004740 0.005966 0.000000
## 4 4 4 Rectifier 0.00 % 0.000000 0.000000 0.252567 0.431084 0.000000
## 5 5 3 Softmax NA 0.000000 0.000000 0.343126 0.454181 0.000000
## mean_weight weight_rms mean_bias bias_rms
## 1 NA NA NA NA
## 2 0.029201 0.611542 0.520232 0.088882
## 3 0.009212 0.385829 1.033779 0.062302
## 4 -0.039279 0.386829 0.981728 0.034980
## 5 -0.683528 1.977224 1.578711 2.693363
##
## H2OMultinomialMetrics: deeplearning
## ** Reported on training data. **
## ** Metrics reported on full training frame **
##
## Training Set Metrics:
## =====================
##
## Extract training frame with `h2o.getFrame("iris_sid_8fd5_1")`
## MSE: (Extract with `h2o.mse`) 0.02359127
## RMSE: (Extract with `h2o.rmse`) 0.1535945
## Logloss: (Extract with `h2o.logloss`) 0.07889532
## Mean Per-Class Error: 0.04
## Confusion Matrix: Extract with `h2o.confusionMatrix(<model>,train = TRUE)`)
## =========================================================================
## Confusion Matrix: Row labels: Actual class; Column labels: Predicted class
## setosa versicolor virginica Error Rate
## setosa 50 0 0 0.0000 = 0 / 50
## versicolor 0 45 5 0.1000 = 5 / 50
## virginica 0 1 49 0.0200 = 1 / 50
## Totals 50 46 54 0.0400 = 6 / 150
##
## Hit Ratio Table: Extract with `h2o.hit_ratio_table(<model>,train = TRUE)`
## =======================================================================
## Top-3 Hit Ratios:
## k hit_ratio
## 1 1 0.960000
## 2 2 1.000000
## 3 3 1.000000
##
##
##
##
##
## Scoring History:
## timestamp duration training_speed epochs iterations
## 1 2020-11-16 12:01:32 0.000 sec NA 0.00000 0
## 2 2020-11-16 12:01:32 0.212 sec 28301 obs/sec 10.00000 1
## 3 2020-11-16 12:01:32 0.261 sec 153061 obs/sec 100.00000 10
## samples training_rmse training_logloss training_r2
## 1 0.000000 NA NA NA
## 2 1500.000000 0.37973 0.44927 0.78371
## 3 15000.000000 0.15359 0.07890 0.96461
## training_classification_error
## 1 NA
## 2 0.14667
## 3 0.04000
##
## Variable Importances: (Extract with `h2o.varimp`)
## =================================================
##
## Variable Importances:
## variable relative_importance scaled_importance percentage
## 1 Petal.Width 1.000000 1.000000 0.342631
## 2 Petal.Length 0.847247 0.847247 0.290294
## 3 Sepal.Width 0.676052 0.676052 0.231637
## 4 Sepal.Length 0.395288 0.395288 0.135438h2o.scoreHistory(model) # see training_classification_error = 100 - acc## Scoring History:
## timestamp duration training_speed epochs iterations
## 1 2020-11-16 12:01:32 0.000 sec NA 0.00000 0
## 2 2020-11-16 12:01:32 0.212 sec 28301 obs/sec 10.00000 1
## 3 2020-11-16 12:01:32 0.261 sec 153061 obs/sec 100.00000 10
## samples training_rmse training_logloss training_r2
## 1 0.000000 NA NA NA
## 2 1500.000000 0.37973 0.44927 0.78371
## 3 15000.000000 0.15359 0.07890 0.96461
## training_classification_error
## 1 NA
## 2 0.14667
## 3 0.04000plot(model)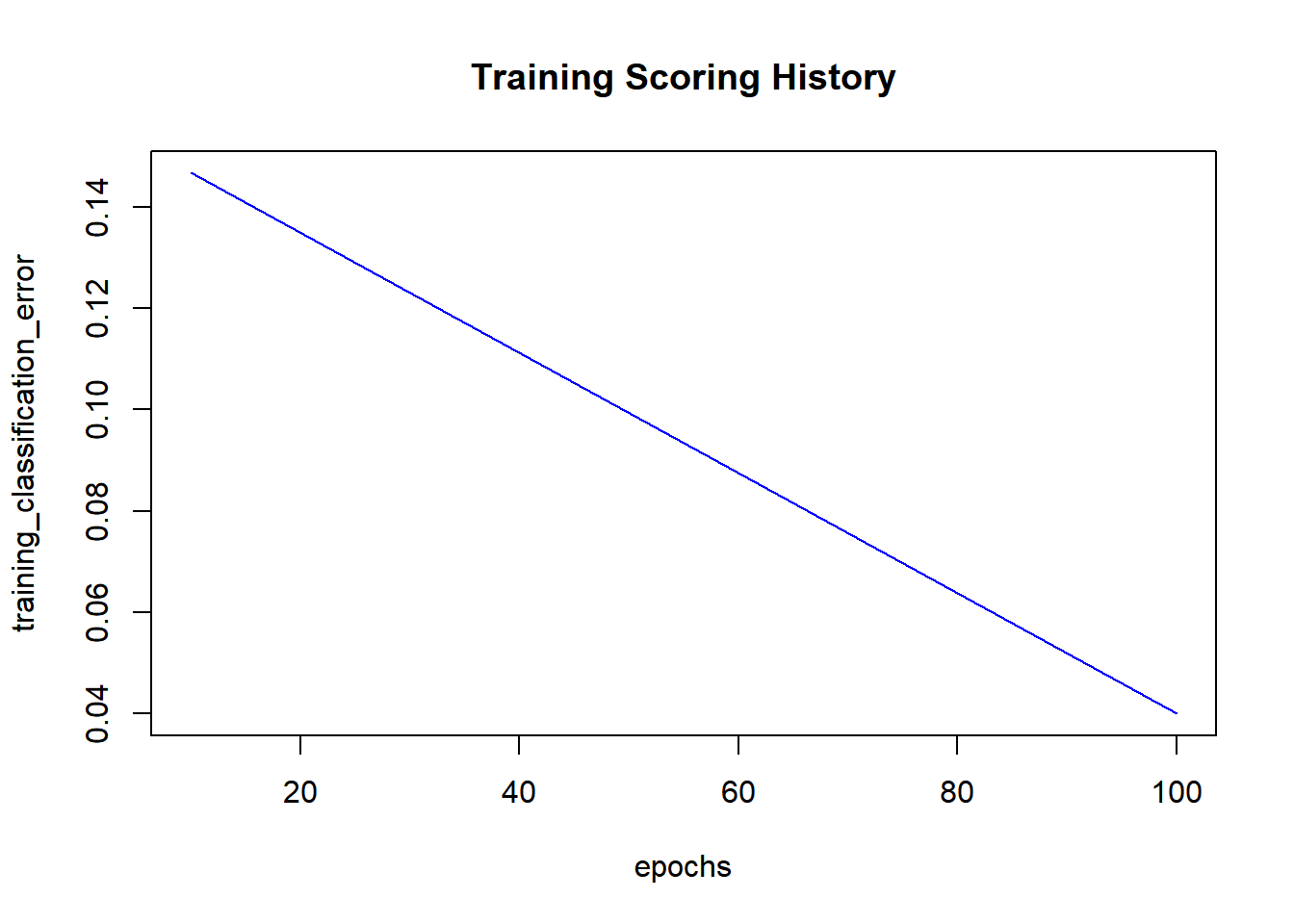
test1 = apply(iris[iris$Species == 'setosa',1:4], 2, mean)
test2 = apply(iris[iris$Species == 'virginica',1:4], 2, mean)
test3 = apply(iris[iris$Species == 'versicolor',1:4], 2, mean)
test = rbind(test1,test2,test3)
newdata = h2o.predict(model,
as.h2o(test))##
|
| | 0%
|
|======================================================================| 100%
##
|
| | 0%
|
|======================================================================| 100%pred = as.data.frame(newdata$predict) # Formal class H2O... need to be converted
print(pred)## predict
## 1 setosa
## 2 virginica
## 3 versicolor10.9 Exercício
Empregue o template de uso do pacote neuralnet para o data set college e implemente o modelo para o conjunto iris. Lembre-se de empregar
RNGversion('3.5.0')
set.seed(1984)Empregue as mesmas configurações da rede no modelo e não faça o rescale dos dados.
10.10 Exercício
Empregue o template de uso do pacote H2o para o data set iris e implemente o modelo para o conjunto fraud.
O dataset fraud encontra-se em:
(http://meusite.mackenzie.br/rogerio/ML/qconlondon2016_sample_data.csv', header=TRUE)Você deve alterar o modelo para contemplar os conjuntos de treinamento (2/3) e teste (1/3) como temos empregado. Também, não empregue o atributo fraud$charge_time no modelo (veja que todas as operações são no mesmo horário).
Altere o modelo certificando-se dos seguintes parâmetros:
epochs=500,
classification_stop=0.4,
hidden=c(4,16,4)Lembre-se de empregar
RNGversion('3.5.0')
set.seed(1984)Veja que mesmo com o seed o treinamento da rede (que gera grupos de treinamento e teste internamente para treinar o modelo) pode apresentar resultados diferentes a cada execução. Respeite portanto os parâmetros dados e as recomendações nas questões sobre execuções sucessivas.