Chapter 4 Visualizar os Dados
4.1 Por que visualizar os dados?
O Quarteto de Anscombe (F.J. Anscombe, 1973) talvez seja o exemplo mais conhecido que ilustra o valor da visualização dos dados.
Os quatro conjuntos de dados exibidos abaixo, pares \((x,y)\), apresentam com até 3 casas decimais as mesmas médias e variâncias de \(x\) e \(y\) e correlação de 0.816, levando todos a uma mesma regressão linear.
\[y = 3 + 0.5 x\]
# note, não é necessário você compreender os detalhes deste código aqui,
# o interesse está no gráfico produzido
require(stats); require(graphics)
summary(anscombe)## x1 x2 x3 x4 y1
## Min. : 4.0 Min. : 4.0 Min. : 4.0 Min. : 8 Min. : 4.260
## 1st Qu.: 6.5 1st Qu.: 6.5 1st Qu.: 6.5 1st Qu.: 8 1st Qu.: 6.315
## Median : 9.0 Median : 9.0 Median : 9.0 Median : 8 Median : 7.580
## Mean : 9.0 Mean : 9.0 Mean : 9.0 Mean : 9 Mean : 7.501
## 3rd Qu.:11.5 3rd Qu.:11.5 3rd Qu.:11.5 3rd Qu.: 8 3rd Qu.: 8.570
## Max. :14.0 Max. :14.0 Max. :14.0 Max. :19 Max. :10.840
## y2 y3 y4
## Min. :3.100 Min. : 5.39 Min. : 5.250
## 1st Qu.:6.695 1st Qu.: 6.25 1st Qu.: 6.170
## Median :8.140 Median : 7.11 Median : 7.040
## Mean :7.501 Mean : 7.50 Mean : 7.501
## 3rd Qu.:8.950 3rd Qu.: 7.98 3rd Qu.: 8.190
## Max. :9.260 Max. :12.74 Max. :12.500##-- now some "magic" to do the 4 regressions in a loop:
ff <- y ~ x
mods <- setNames(as.list(1:4), paste0("lm", 1:4))
for(i in 1:4) {
ff[2:3] <- lapply(paste0(c("y","x"), i), as.name)
## or ff[[2]] <- as.name(paste0("y", i))
## ff[[3]] <- as.name(paste0("x", i))
mods[[i]] <- lmi <- lm(ff, data = anscombe)
print(anova(lmi))
}## Analysis of Variance Table
##
## Response: y1
## Df Sum Sq Mean Sq F value Pr(>F)
## x1 1 27.510 27.5100 17.99 0.00217 **
## Residuals 9 13.763 1.5292
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Analysis of Variance Table
##
## Response: y2
## Df Sum Sq Mean Sq F value Pr(>F)
## x2 1 27.500 27.5000 17.966 0.002179 **
## Residuals 9 13.776 1.5307
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Analysis of Variance Table
##
## Response: y3
## Df Sum Sq Mean Sq F value Pr(>F)
## x3 1 27.470 27.4700 17.972 0.002176 **
## Residuals 9 13.756 1.5285
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Analysis of Variance Table
##
## Response: y4
## Df Sum Sq Mean Sq F value Pr(>F)
## x4 1 27.490 27.4900 18.003 0.002165 **
## Residuals 9 13.742 1.5269
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## See how close they are (numerically!)
sapply(mods, coef)## lm1 lm2 lm3 lm4
## (Intercept) 3.0000909 3.000909 3.0024545 3.0017273
## x1 0.5000909 0.500000 0.4997273 0.4999091lapply(mods, function(fm) coef(summary(fm)))## $lm1
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.0000909 1.1247468 2.667348 0.025734051
## x1 0.5000909 0.1179055 4.241455 0.002169629
##
## $lm2
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.000909 1.1253024 2.666758 0.025758941
## x2 0.500000 0.1179637 4.238590 0.002178816
##
## $lm3
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.0024545 1.1244812 2.670080 0.025619109
## x3 0.4997273 0.1178777 4.239372 0.002176305
##
## $lm4
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.0017273 1.1239211 2.670763 0.025590425
## x4 0.4999091 0.1178189 4.243028 0.002164602## Now, do what you should have done in the first place: PLOTS
op <- par(mfrow = c(2, 2), mar = 0.1+c(4,4,1,1), oma = c(0, 0, 2, 0))
for(i in 1:4) {
ff[2:3] <- lapply(paste0(c("y","x"), i), as.name)
plot(ff, data = anscombe, col = "red", pch = 21, bg = "orange", cex = 1.2,
xlim = c(3, 19), ylim = c(3, 13))
abline(mods[[i]], col = "blue")
}
mtext("Anscombe's 4 Regression data sets", outer = TRUE, cex = 1.5)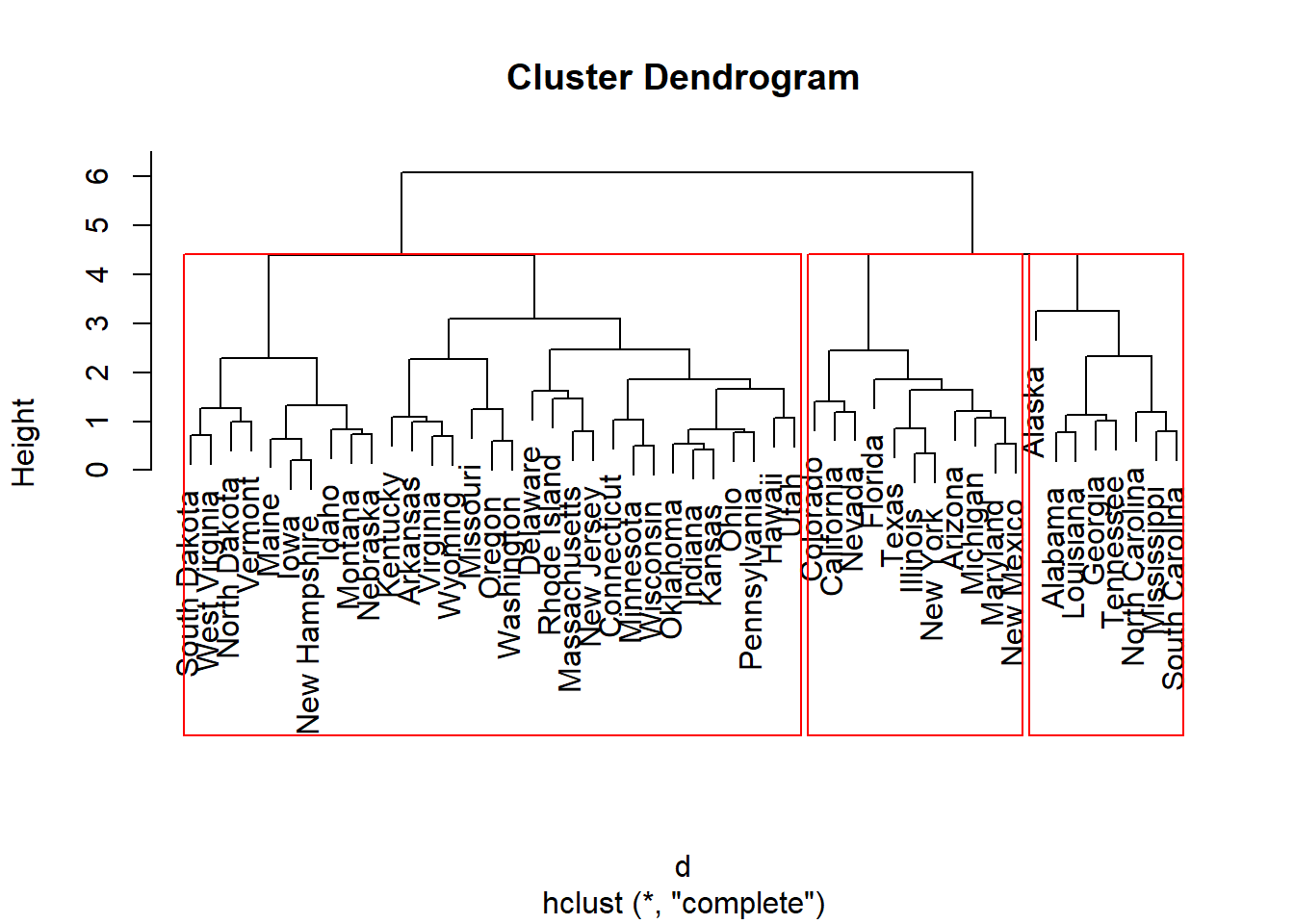
par(op)4.2 Buscando gráficos corretos
As perguntas que podemos fazer sobre os dados podem ser agrupadas em algumas categorias relevantes, cada uma delas tendo gráficos mais adequados para você obter e apresentar respostas à sua questão:
Evolução (ou Tendência dos Dados): gráficos de linha, área, séries múltiplas
Distribuição: histogramas, gráficos de distribuição de densidade, boxplot
Ranking: gráficos de barras, word cloud, spider
Correlação: gráficos de dispersão, heat map, density 2D
Partes de um todo: Tree map, diagramas Venn, pie chart
Havendo ainda gráficos especializados que envolvem para análises geográficas (maps) ou fluxo de dados em redes sociais.
4.3 Evolução
Muitos dados apresentam uma evolução ao longo tempo. Nesses casos, frequentemente queremos saber sobre a tendência dessa evolução, sobre a probabilidade de se alcançar um valor ou ainda comparar a forma de evolução de variáveis que possam ter alguma relação.
Quando essas variáveis são numéricas um gráfico de linhas é frequentemente usado para visualizar a tendência nos dados em intervalos de tempo e responder essas perguntas.
Considere a base.
df = read.csv('http://meusite.mackenzie.br/rogerio/TIC/mystocksn.csv')
head(df)## data IBOV VALE3 PETR4 DOLAR
## 1 2020-01-02 118573 13.45 16.27 4.0163
## 2 2020-01-03 117707 13.29 15.99 4.0234
## 3 2020-01-06 116878 13.14 16.22 4.0570
## 4 2020-01-07 116662 13.23 16.06 4.0604
## 5 2020-01-08 116247 13.22 15.70 4.0662
## 6 2020-01-09 115947 12.99 15.75 4.0628df$data = factor(df$data) # necessário após atualizaçao do RCloud em Maio.2020plot dos valores (x,y)
par(mfrow = c(2, 2))
plot(df$data,df$IBOV)
plot(df$data,df$VALE3)
plot(df$data,df$PETR4)
plot(df$data,df$DOLAR)
plot(df$data,df$DOLAR, main='Evolução do Dólar',ylim=c(3,8),ylabel='Dólar')
abline(h=4.3,col='red')
help(plot)## starting httpd help server ... done4.4 Distribuição
Os dados a seguir foram obtidos da WHO World Health Organization - Life expectancy and Healthy life expecancy. Eles apresentam indicadores de saúde de diversos países como o índice de massa corpórea médio da população (BMI), a expectativa de vida e índices de mortalidade. Uma pergunta relevante sobre a saúde global poderia ser sobre a distribuição de certos índices entre os países, como por exemplo o caso a seguir.
Considere a base.
df = read.csv('https://meusite.mackenzie.br/rogerio/TIC/Life_Expectancy_Data.csv')
head(df)## Country Year Status Life.expectancy Adult.Mortality infant.deaths
## 1 Afghanistan 2015 Developing 65.0 263 62
## 2 Afghanistan 2014 Developing 59.9 271 64
## 3 Afghanistan 2013 Developing 59.9 268 66
## 4 Afghanistan 2012 Developing 59.5 272 69
## 5 Afghanistan 2011 Developing 59.2 275 71
## 6 Afghanistan 2010 Developing 58.8 279 74
## Alcohol percentage.expenditure Hepatitis.B Measles BMI under.five.deaths
## 1 0.01 71.279624 65 1154 19.1 83
## 2 0.01 73.523582 62 492 18.6 86
## 3 0.01 73.219243 64 430 18.1 89
## 4 0.01 78.184215 67 2787 17.6 93
## 5 0.01 7.097109 68 3013 17.2 97
## 6 0.01 79.679367 66 1989 16.7 102
## Polio Total.expenditure Diphtheria HIV.AIDS GDP Population
## 1 6 8.16 65 0.1 584.25921 33736494
## 2 58 8.18 62 0.1 612.69651 327582
## 3 62 8.13 64 0.1 631.74498 31731688
## 4 67 8.52 67 0.1 669.95900 3696958
## 5 68 7.87 68 0.1 63.53723 2978599
## 6 66 9.20 66 0.1 553.32894 2883167
## thinness..1.19.years thinness.5.9.years Income.composition.of.resources
## 1 17.2 17.3 0.479
## 2 17.5 17.5 0.476
## 3 17.7 17.7 0.470
## 4 17.9 18.0 0.463
## 5 18.2 18.2 0.454
## 6 18.4 18.4 0.448
## Schooling
## 1 10.1
## 2 10.0
## 3 9.9
## 4 9.8
## 5 9.5
## 6 9.2library(lattice)
par(mfrow = c(2, 1))
hist(df$Life.expectancy, main='Expectativa de Vida dos Países')
hist(df$Life.expectancy, main='Expectativa de Vida dos Países', breaks = 100, col = "lightblue", freq=TRUE)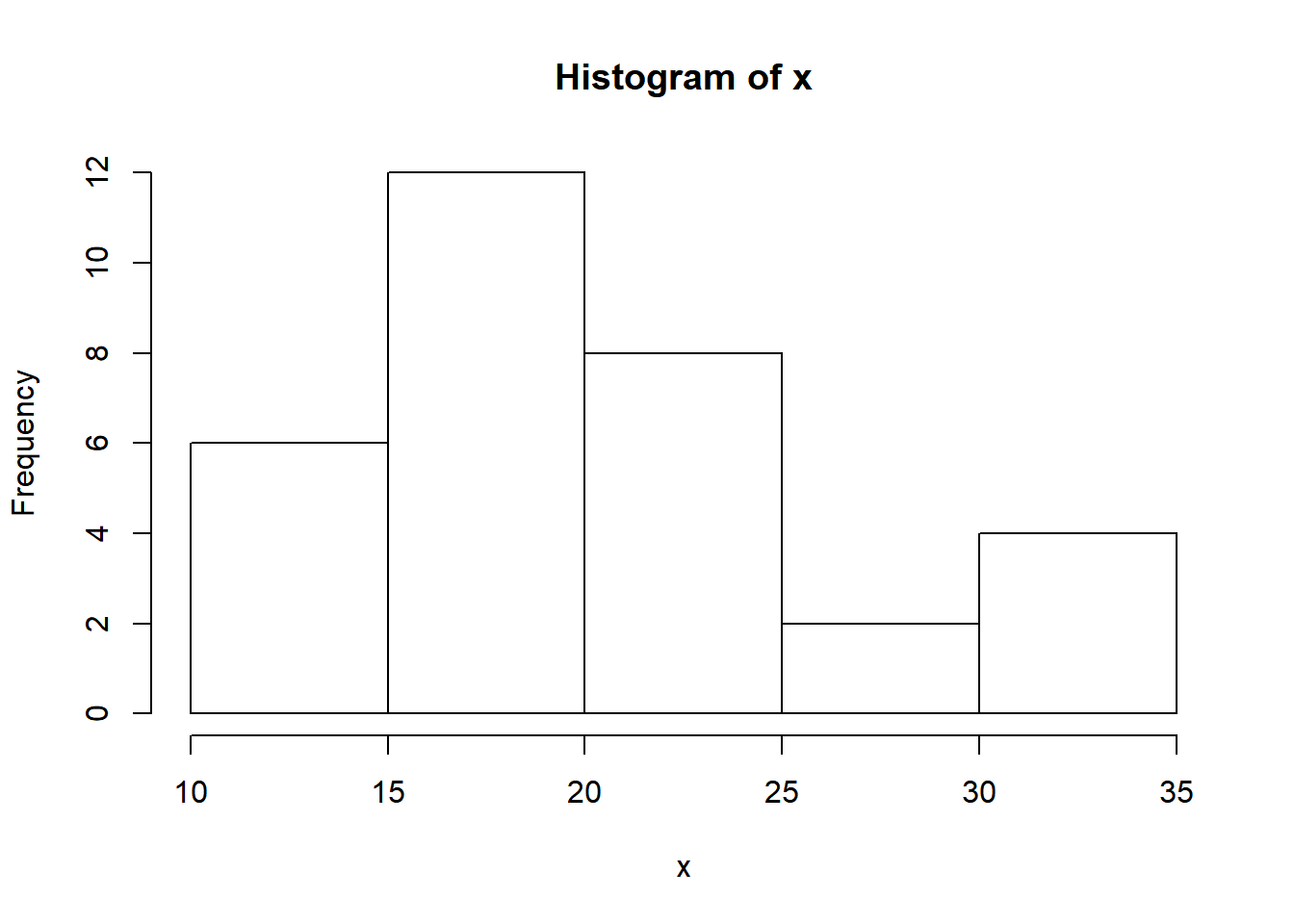
densityplot(df$Life.expectancy, main='Expectativa de Vida dos Países')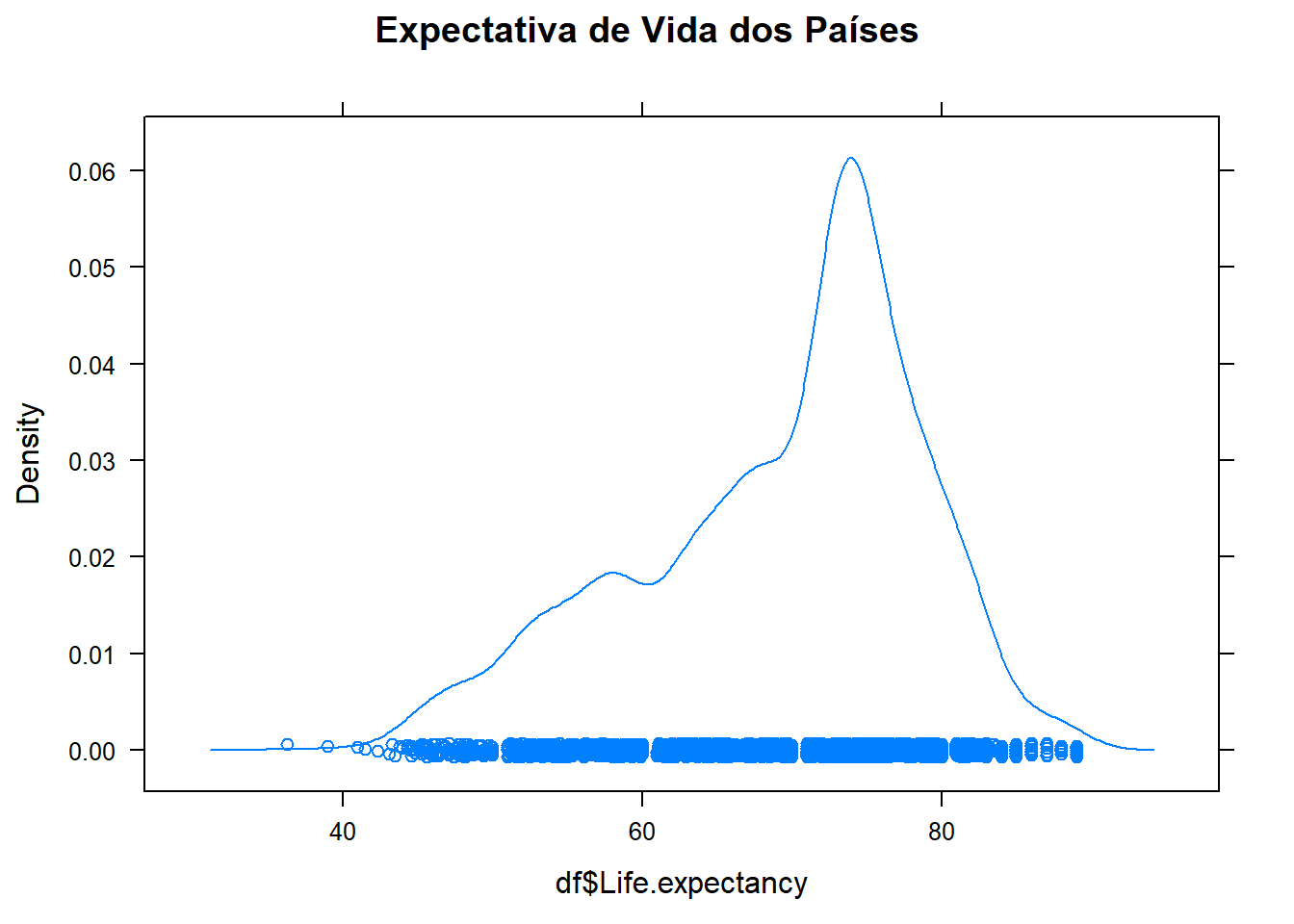
help(plot)d = density(df$Life.expectancy,na.rm = TRUE)
plot(d, main="Expectativa de Vida")
polygon(d, col="orange", border="black")
par(mfrow = c(1, 3))
boxplot(df$Life.expectancy,main='Expectativa de Vida')
boxplot(df$BMI,main='BMI')
boxplot(Life.expectancy ~ Status,data=df,main="Expectativa de Vida ")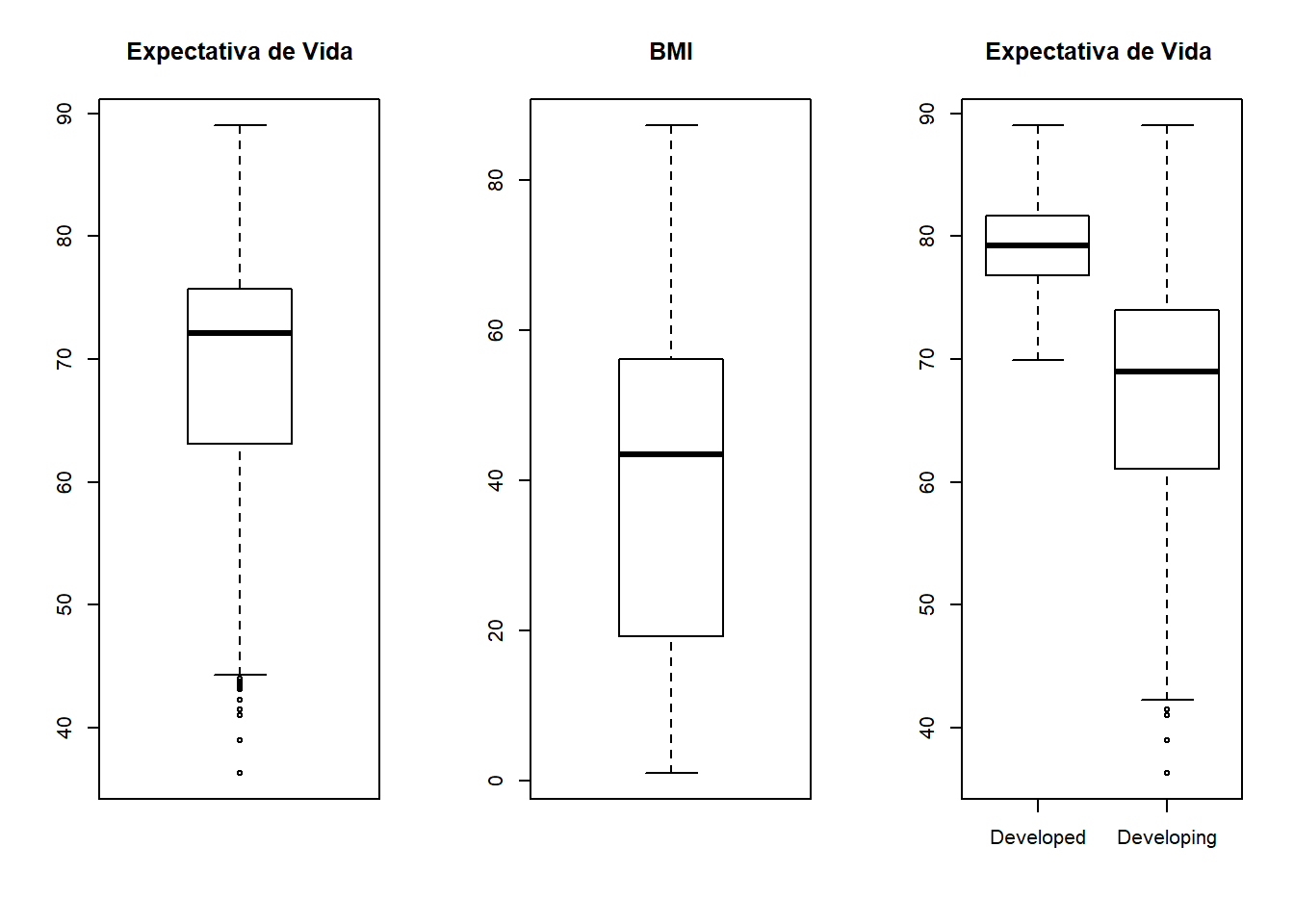
4.5 Correlação
Relações entre os dados são muitas vezes a parte mais importante dentre as descobertas que buscamos nos dados. Essas relações em geral são denominadas de modo geral como correlações. Mas é importante notar que a correlação estatística tem um significado muito mais específico e, em geral, está associada a correlação linear. Graficamente, entretanto, estamos livres para buscar quaisquer relações entre os dados, sejam elas lineares ou não.
Considere a base.
df = read.csv('https://meusite.mackenzie.br/rogerio/TIC/Pokemon.csv')
head(df)## X. Name Type.1 Type.2 Total HP Attack Defense Sp..Atk
## 1 1 Bulbasaur Grass Poison 318 45 49 49 65
## 2 2 Ivysaur Grass Poison 405 60 62 63 80
## 3 3 Venusaur Grass Poison 525 80 82 83 100
## 4 3 VenusaurMega Venusaur Grass Poison 625 80 100 123 122
## 5 4 Charmander Fire 309 39 52 43 60
## 6 5 Charmeleon Fire 405 58 64 58 80
## Sp..Def Speed Generation Legendary
## 1 65 45 1 False
## 2 80 60 1 False
## 3 100 80 1 False
## 4 120 80 1 False
## 5 50 65 1 False
## 6 65 80 1 Falsepairs(df)
pairs(df[,c(5:8)])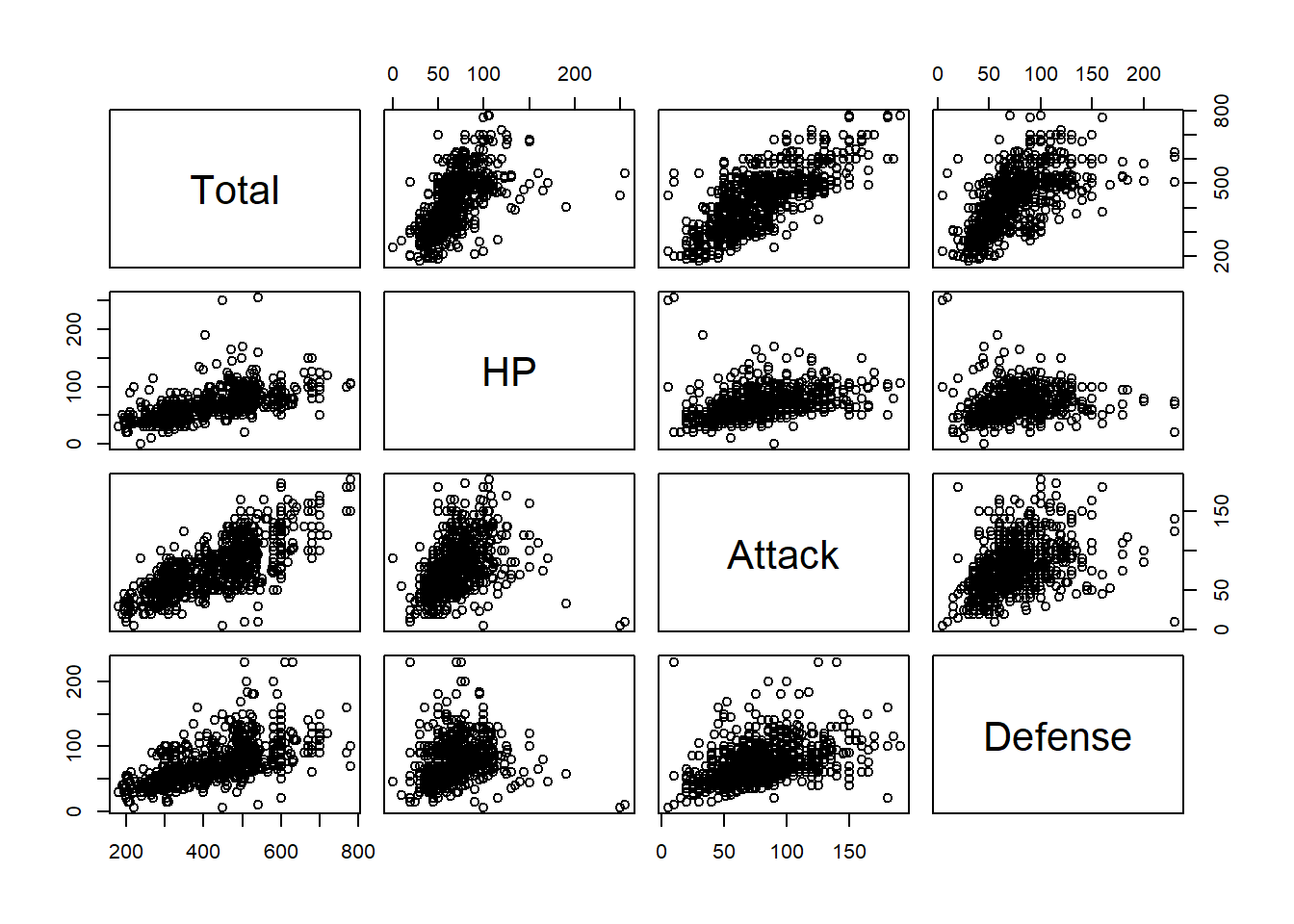
plot(df[,c(5,7)])
abline(lsfit(df[,5],df[,7]),col='red')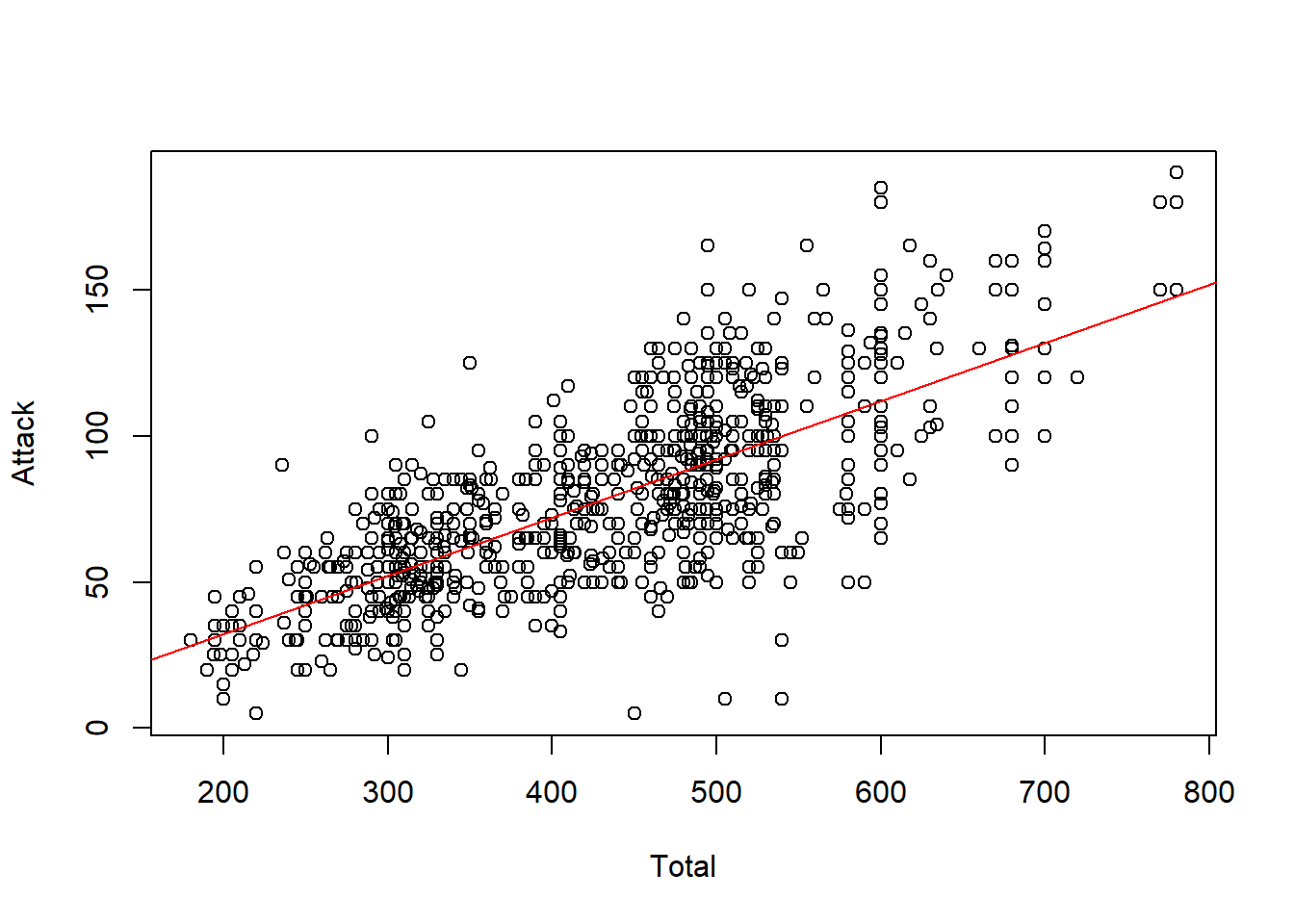
boxplot(Total ~ Generation,data=df, main="Total by Generation")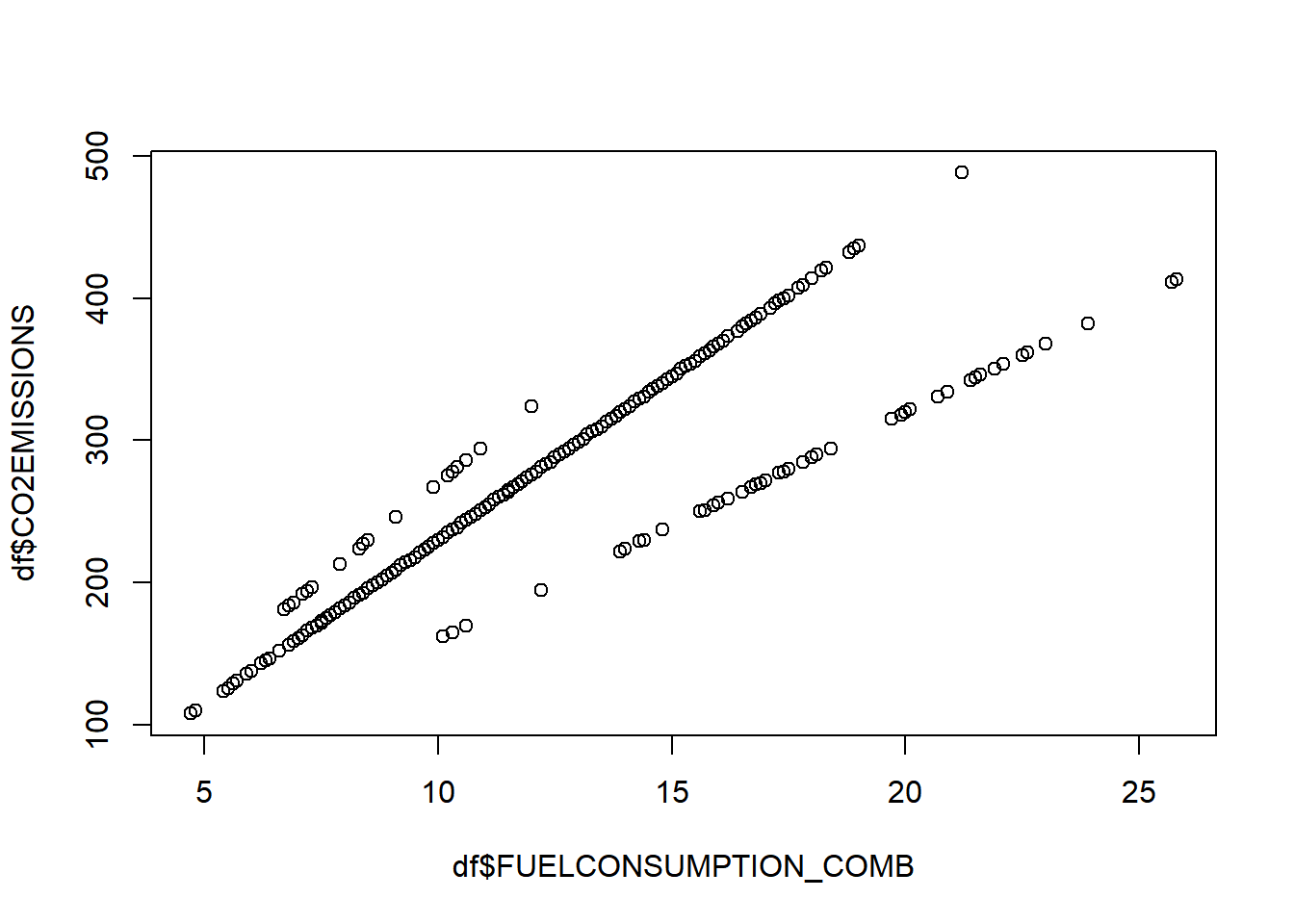
4.6 Ranking
Comparar quantidades de diferentes categorias é uma tarefa frequente e útil. Responde a perguntas de maiores, menores valores, mais e menos presentes.
Considere a base.
help(mtcars)
head(mtcars)## mpg cyl disp hp drat wt qsec vs am gear carb
## Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
## Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
## Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
## Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
## Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
## Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1par(mfrow = c(1, 3))
counts = table(mtcars$gear)
barplot(counts, main="Distribuição dos Veículos", xlab="Número de Marchas",
col='darkblue')
pie(table(mtcars$cyl), main="Distribuição dos Veículos", xlab="Número de Cilindros")
dotchart(mtcars$hp,labels=row.names(mtcars),cex=.7,col='orange',
main="Potência dos Modelos",
xlab="hp")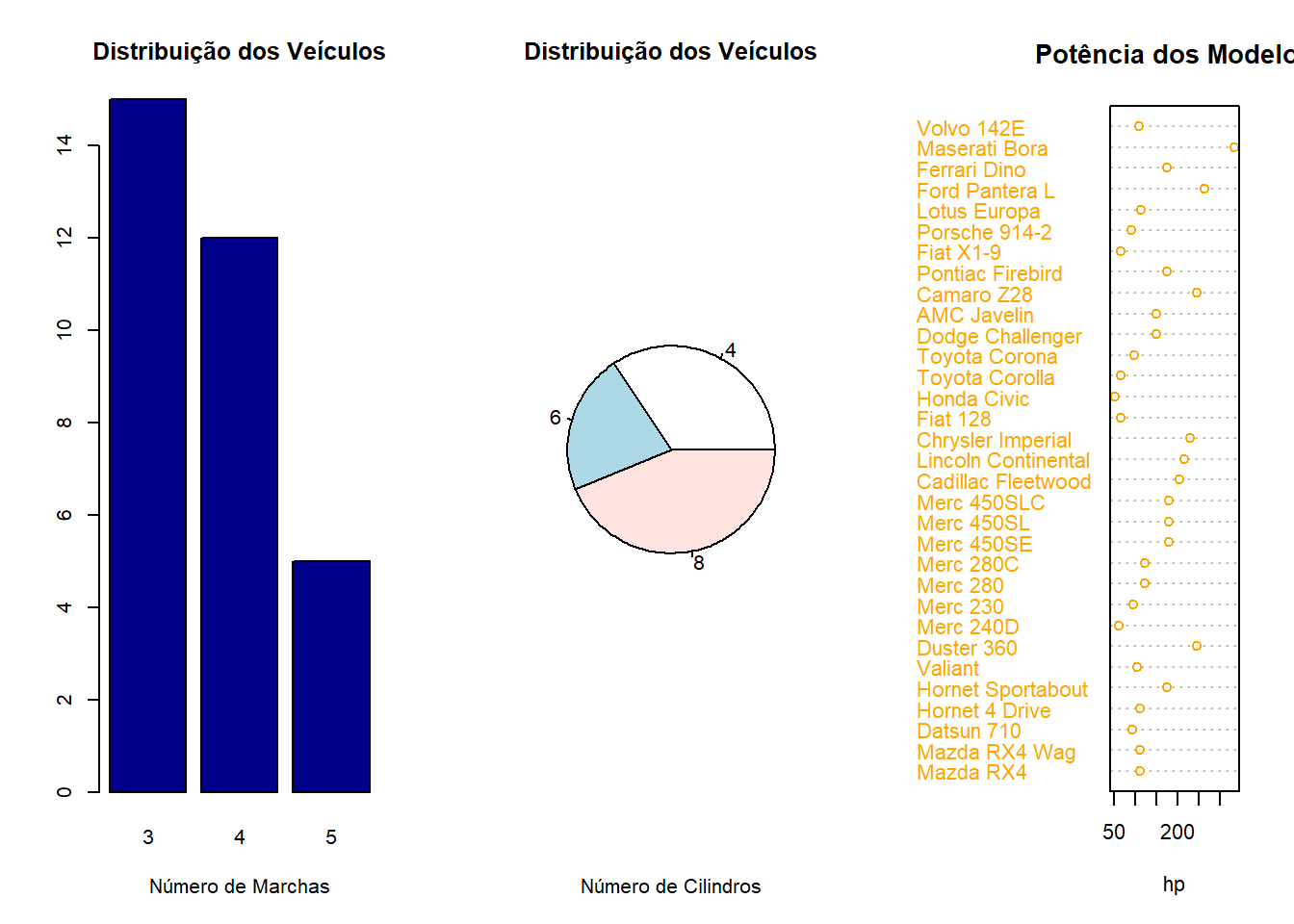
# Grouped Bar Plot
counts <- table(mtcars$cyl, mtcars$gear)
barplot(counts, main="Número de Marchas vs Cilindros",
xlab="Número de Marchas", col=c("darkblue","orange"),
legend = rownames(counts), beside=TRUE)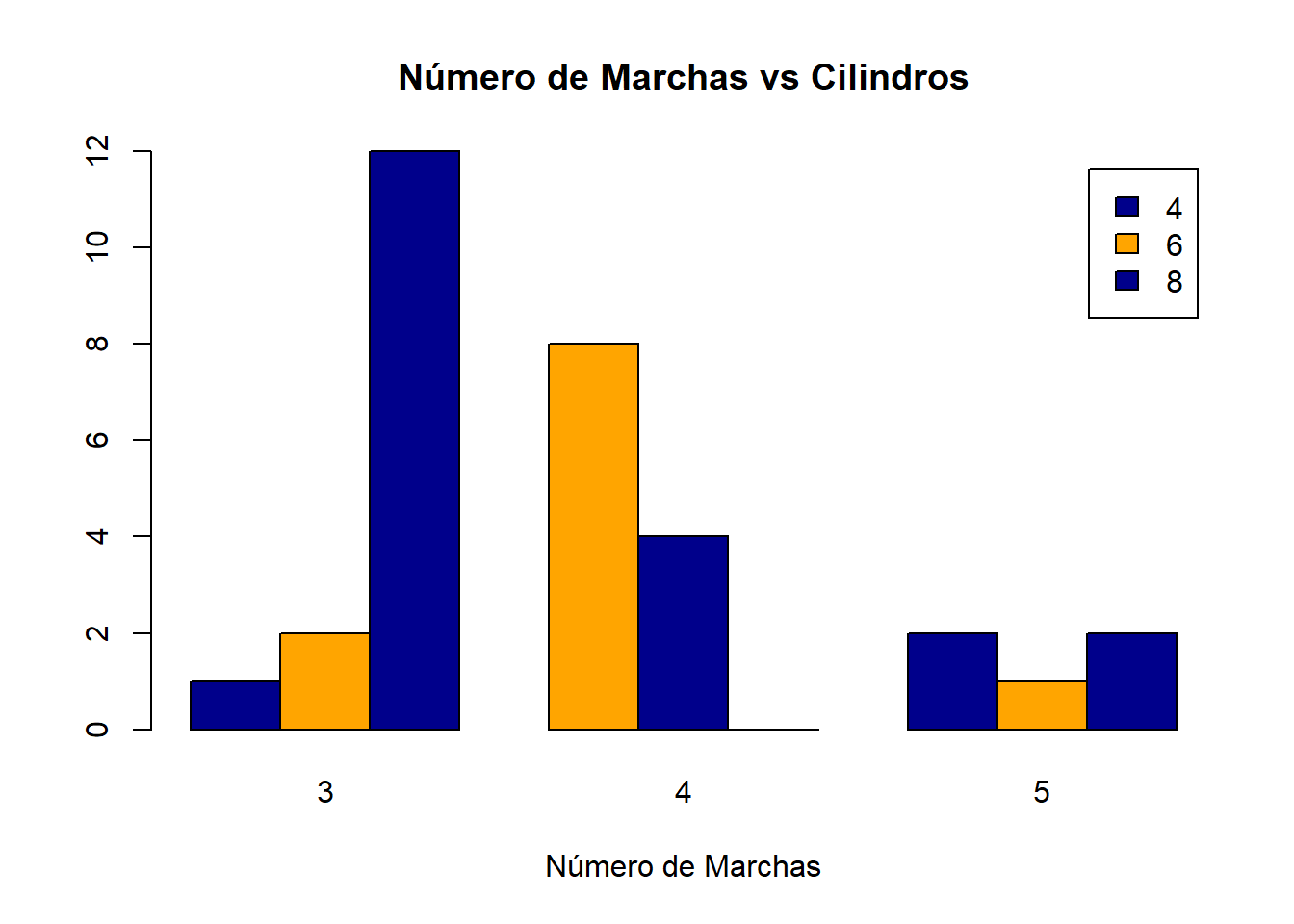
boxplot(mpg~cyl,data=mtcars, main="Consumo vs Cyl",
xlab="Número de Cilindros", ylab="Milhas por Galão",col='blue')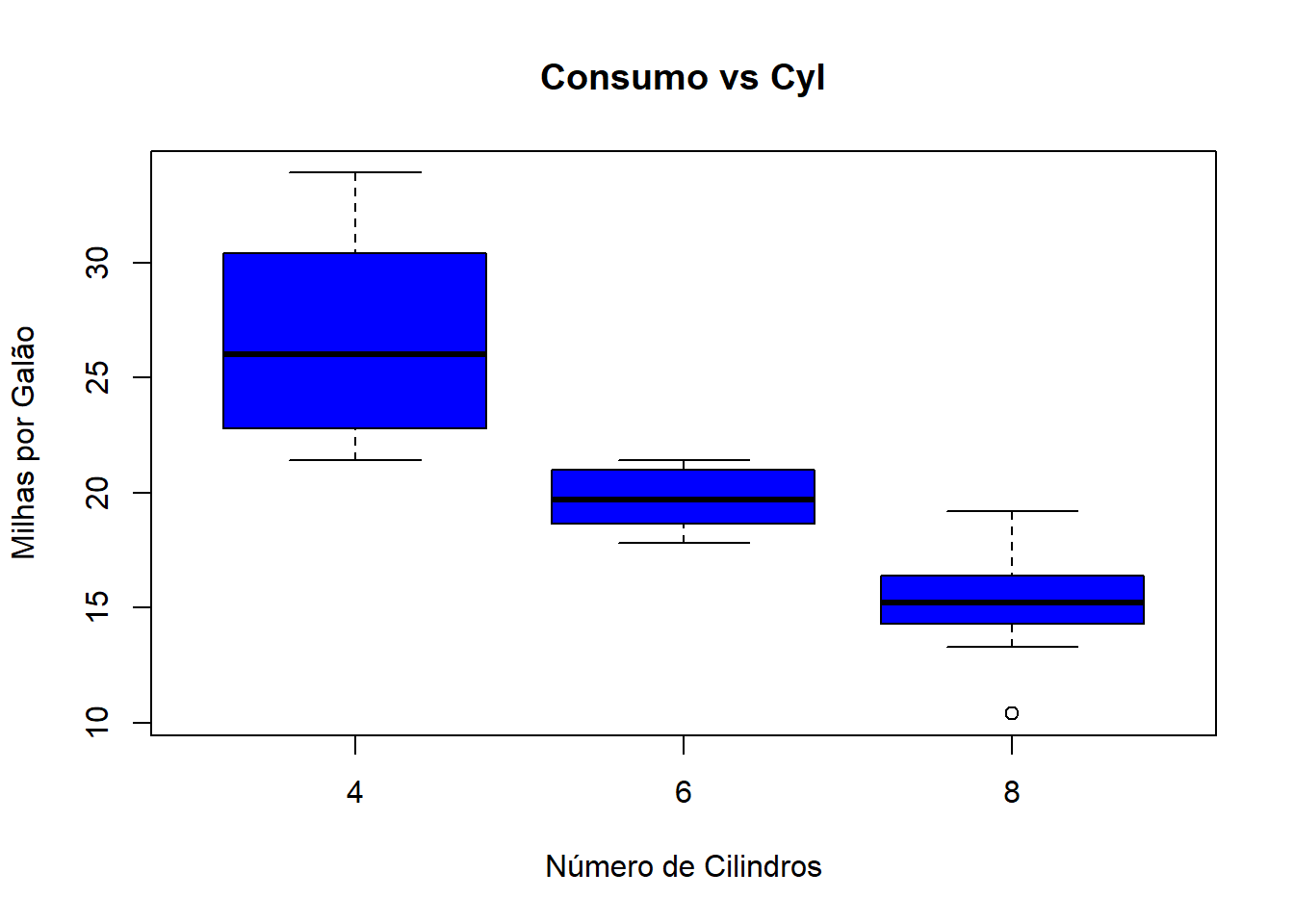
4.7 Melhores Gráficos
Para os nossos propósitos os gráficos acima serão suficientes. Mas se você se interessa por gráficos com uma apresentação mais profissional pode empregar a biblioteca ggplot2.
# install.packages('ggplot2')
# Loading
# library(ggplot2)4.8 Exercícios
4.8.1 Exercício
Considere a base.
data(CPS85 , package = "mosaicData")
head(CPS85)## wage educ race sex hispanic south married exper union age sector
## 1 9.0 10 W M NH NS Married 27 Not 43 const
## 2 5.5 12 W M NH NS Married 20 Not 38 sales
## 3 3.8 12 W F NH NS Single 4 Not 22 sales
## 4 10.5 12 W F NH NS Married 29 Not 47 clerical
## 5 15.0 12 W M NH NS Married 40 Union 58 const
## 6 9.0 16 W F NH NS Married 27 Not 49 clerical4.8.2 Exercício
Faça um histograma e gráficos de caixa de educ e expr. Existem outliers para que valores?
par(mfrow = c(2, 2))
hist(CPS85$educ)
boxplot(CPS85$educ)
hist(CPS85$exper)
boxplot(CPS85$exper)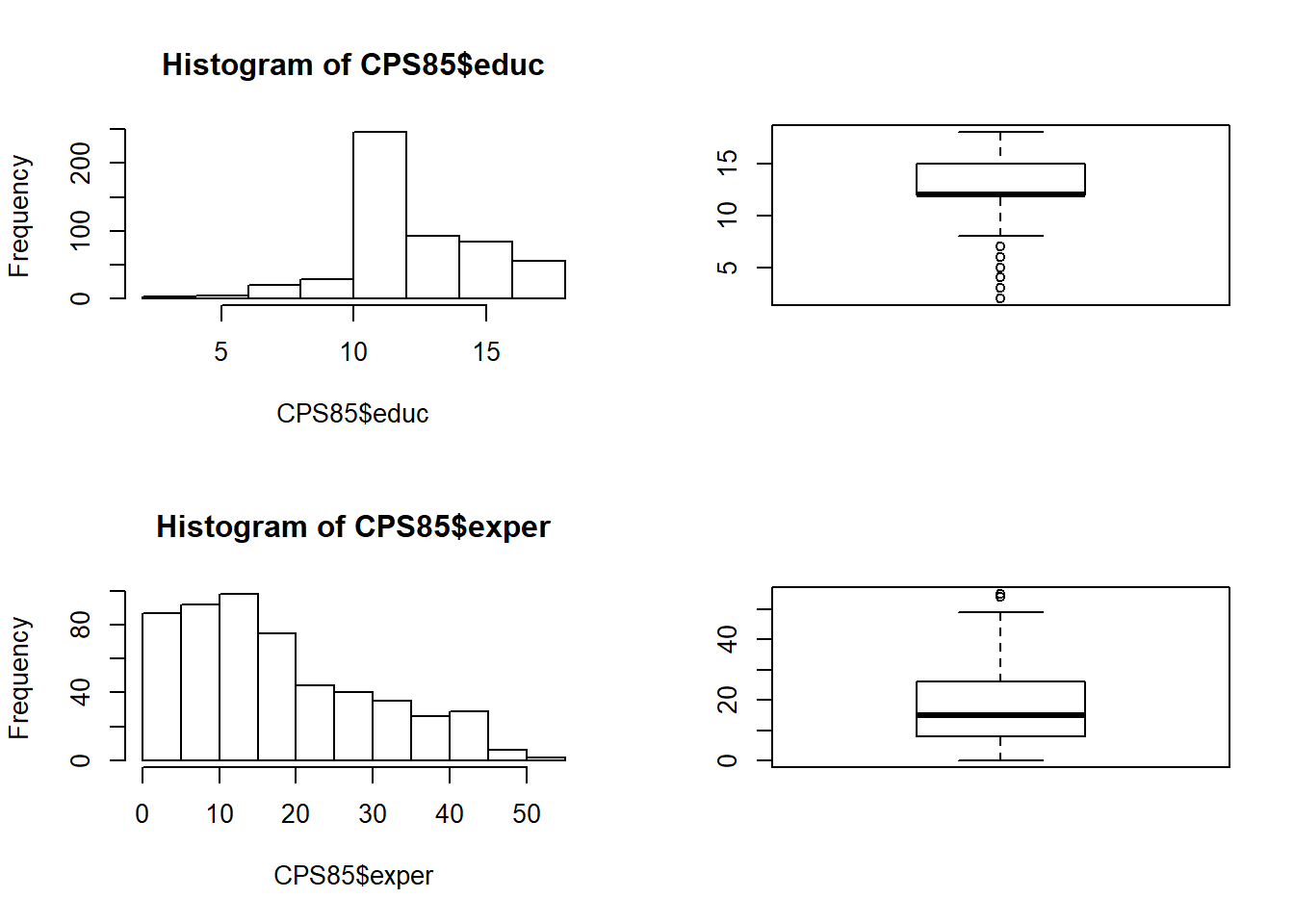
4.8.3 Exercício
Faça gráficos para exibir a distribuição (histograma) de valores de educ, exper e wage separadamente para os sexos Masculino e Feminino. Que distribuições concentram valores mais a esquerda (valores menores)?
par(mfrow = c(3, 2))
hist(CPS85[CPS85$sex == 'M',]$educ)
hist(CPS85[CPS85$sex == 'F',]$educ)
hist(CPS85[CPS85$sex == 'M',]$exper)
hist(CPS85[CPS85$sex == 'F',]$exper)
hist(CPS85[CPS85$sex == 'M',]$wage)
hist(CPS85[CPS85$sex == 'F',]$wage)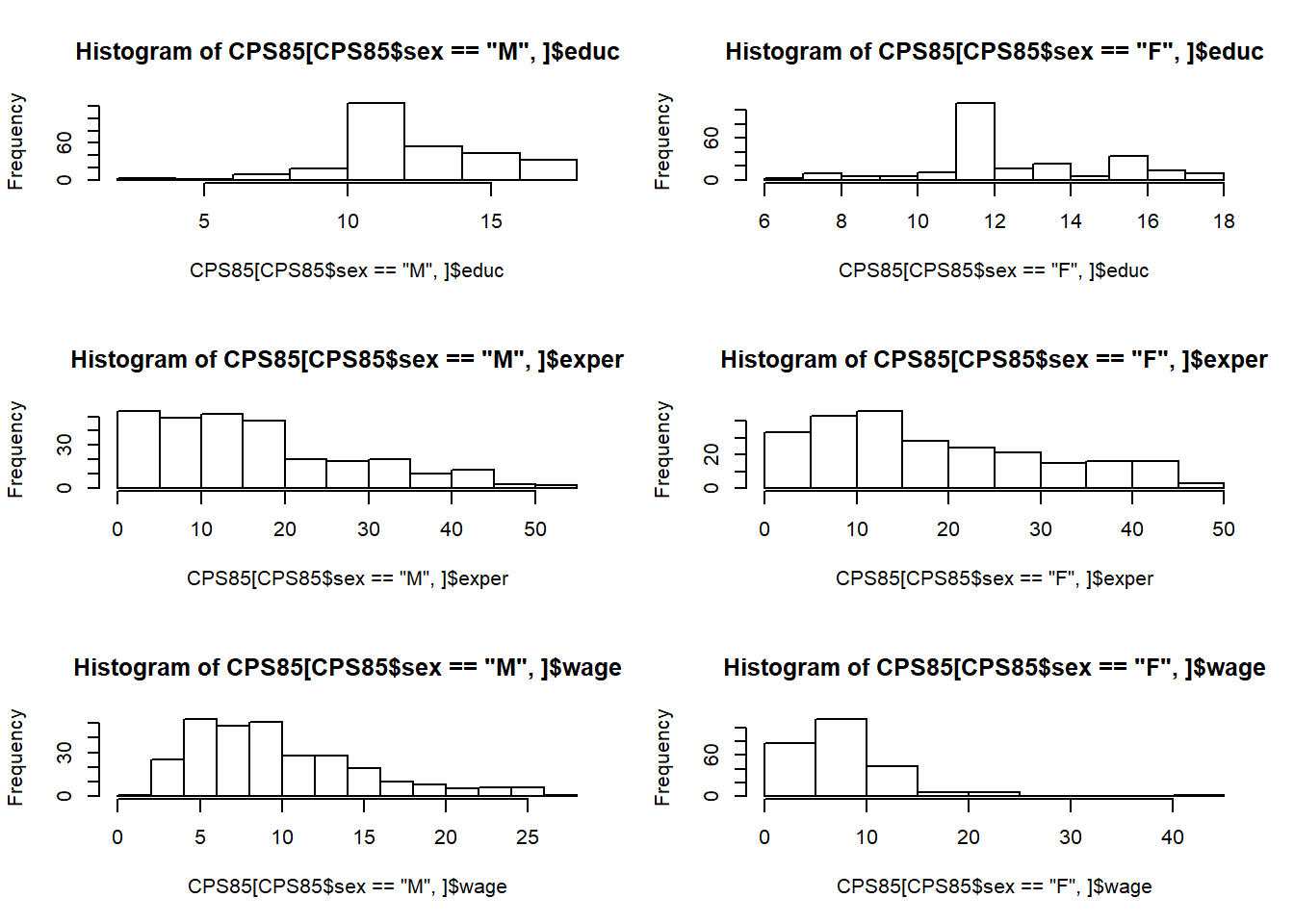
4.8.4 Exercício
Analise a distribuição dos mesmos dados do problema anterior, mas agora empregue um gráfico de caixa e a função ~ para exibir separadamente os sexos.
par(mfrow = c(1, 3))
boxplot(educ ~ sex, data=CPS85, main='educ',col='orange')
boxplot(exper ~ sex, data=CPS85, main='exper',col='green')
boxplot(wage~ sex, data=CPS85, main='wage',col='blue')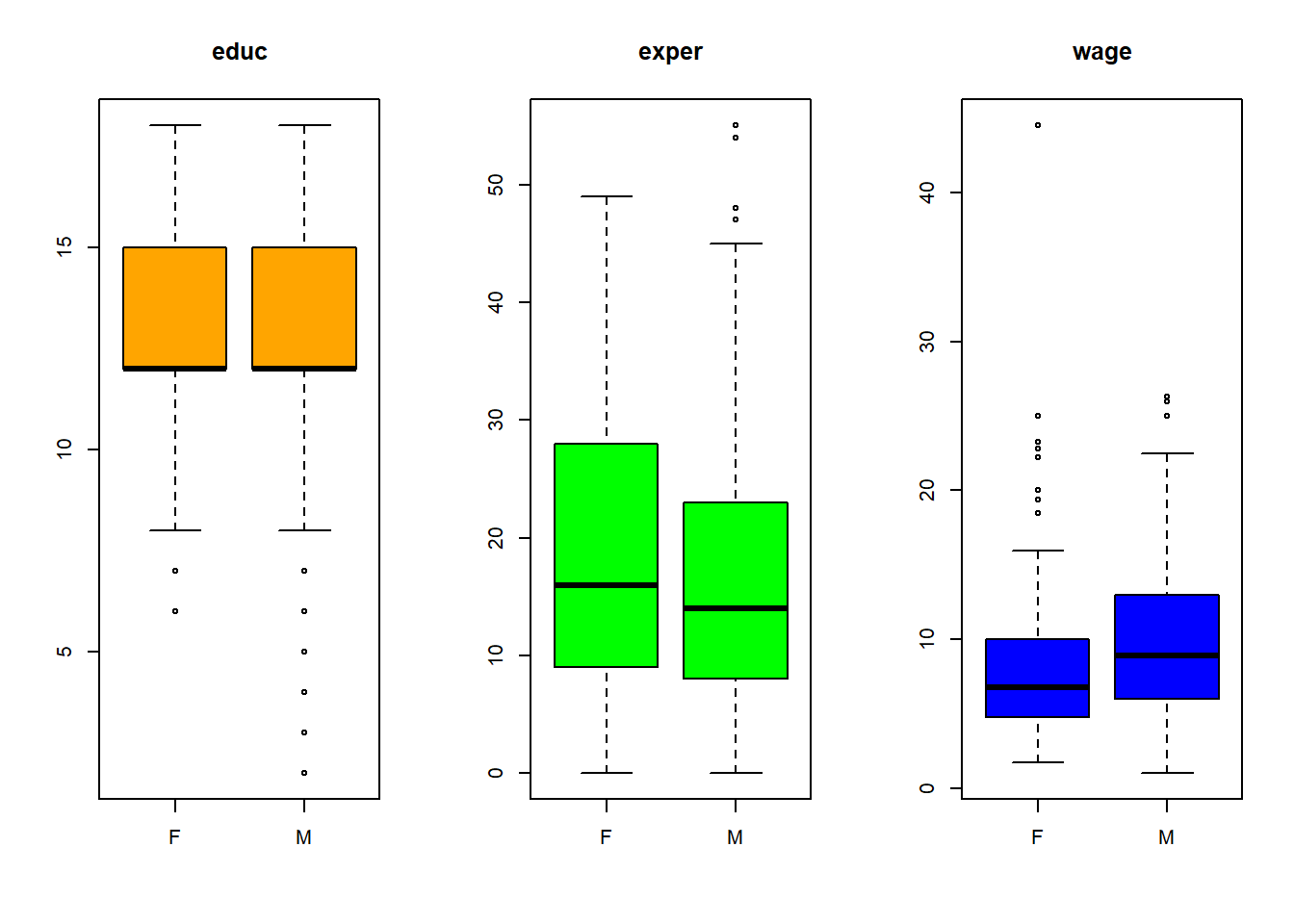
4.8.5 Exercício
Consulte o help do boxplot. Busque uma opção que exiba com maior evidência a mediana e o quanto ela difere dos outros valores. Repita então o exercício anterior com essa opção. Se conseguir (rs) empregue uma opção para colorir diferentemente as caixas para o sexo Feminino e Masculino.
par(mfrow = c(1, 3))
boxplot(educ ~ sex, data=CPS85, main='educ',col=c('pink','blue'),notch=TRUE)## Warning in bxp(list(stats = structure(c(8, 12, 12, 15, 18, 8, 12, 12, 15, : some
## notches went outside hinges ('box'): maybe set notch=FALSEboxplot(exper ~ sex, data=CPS85, main='exper',col=c('pink','blue'),notch=TRUE)
boxplot(wage ~ sex, data=CPS85, main='wage',col=c('pink','blue'),notch=TRUE)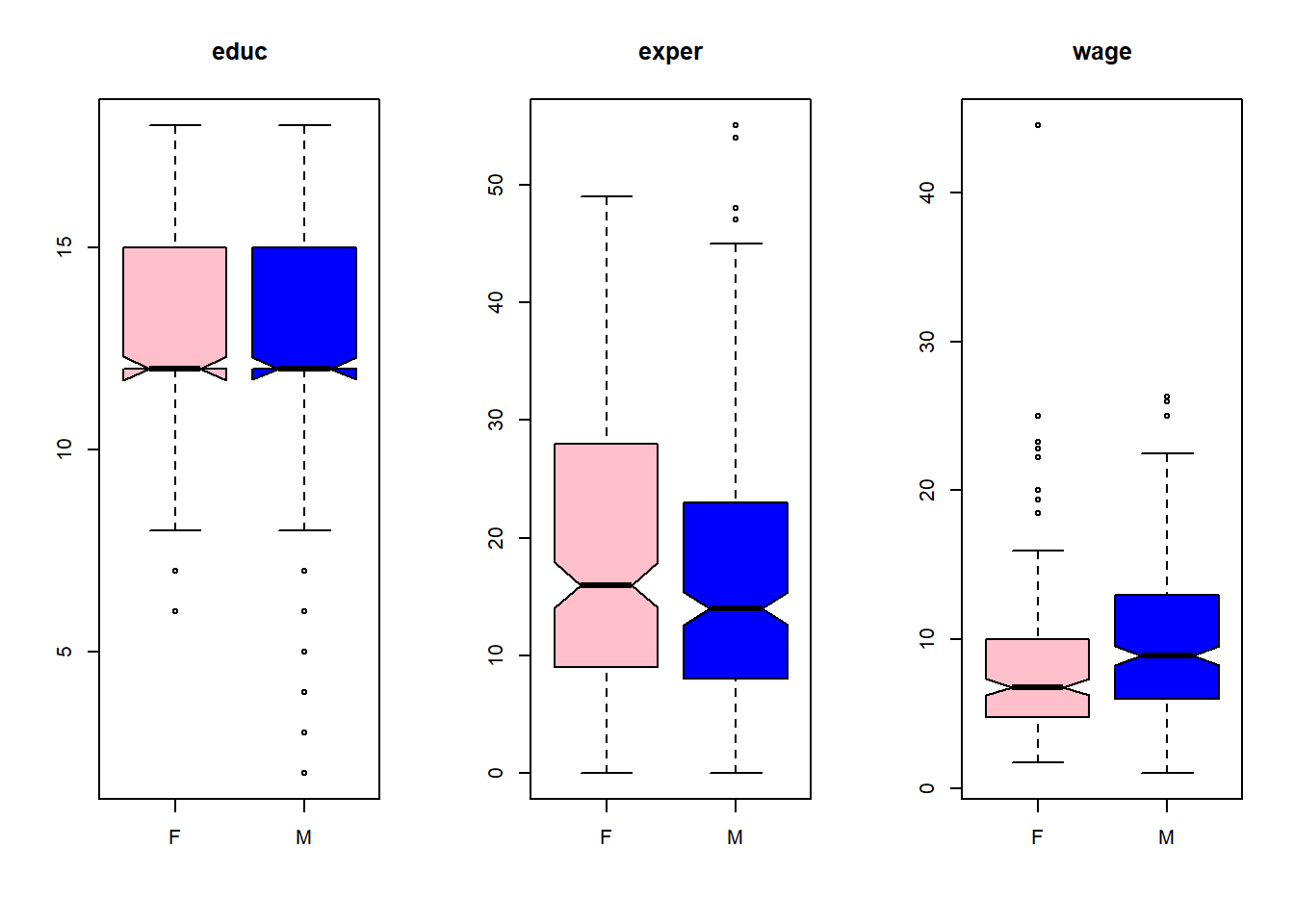
4.8.6 Exercício
Empregue um gráfico de barras e outro de pizza para exibir a proporção de do status de casados na base. Dica: para o pie() você precisa fornecer a frequencia dos valores. Empregue em conjunto o table().
par(mfrow = c(1, 2))
barplot(table(CPS85$married),col='green')
pie(table(CPS85$married))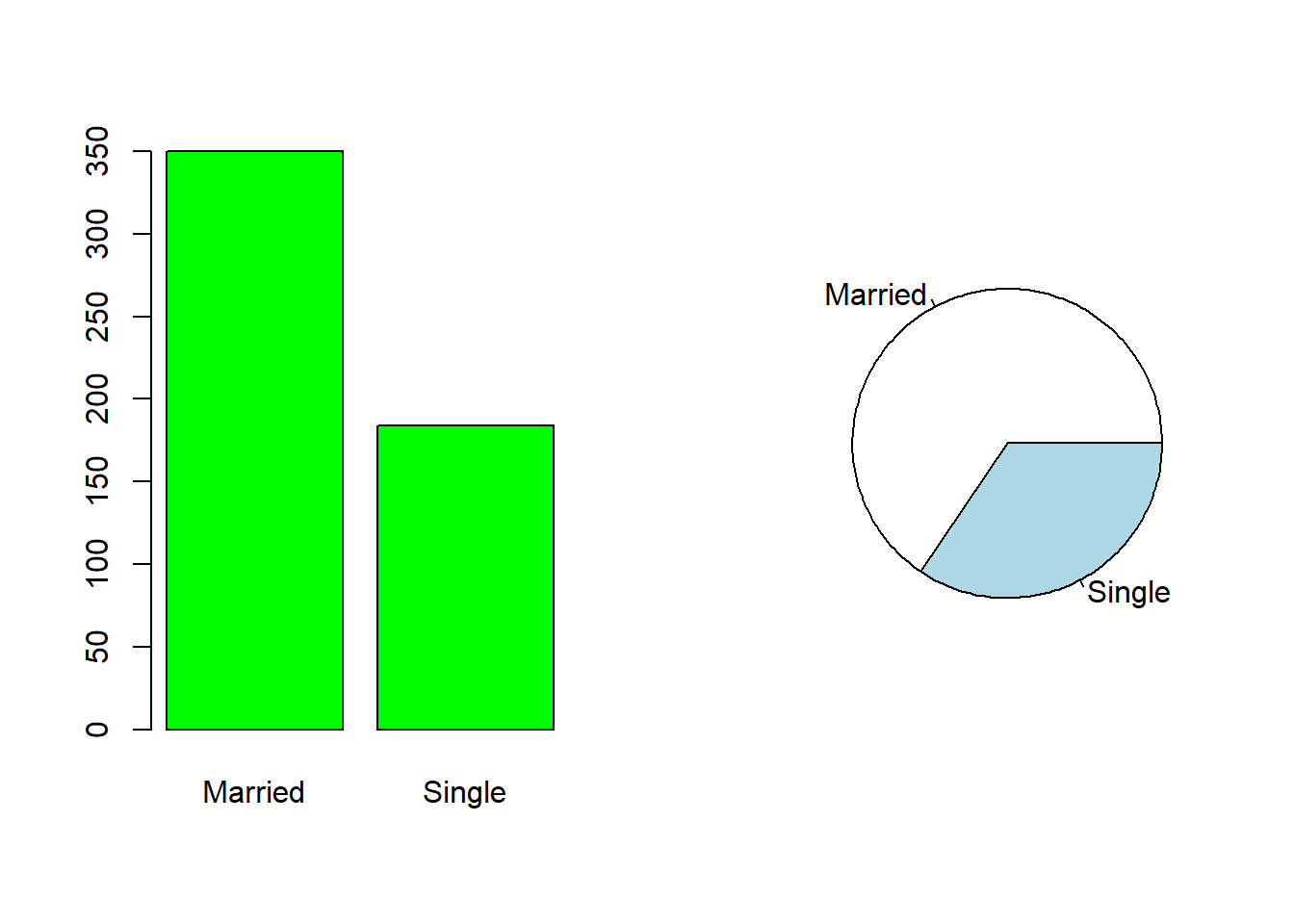 
4.8.7 Exercício
Faça um gráfico de densidade e um histogram com breaks=30 para os valores de rendimentos (wage). Compare os gráficos.
par(mfrow = c(1, 2))
hist(CPS85$wage,breaks=30)
densityplot(CPS85$wage)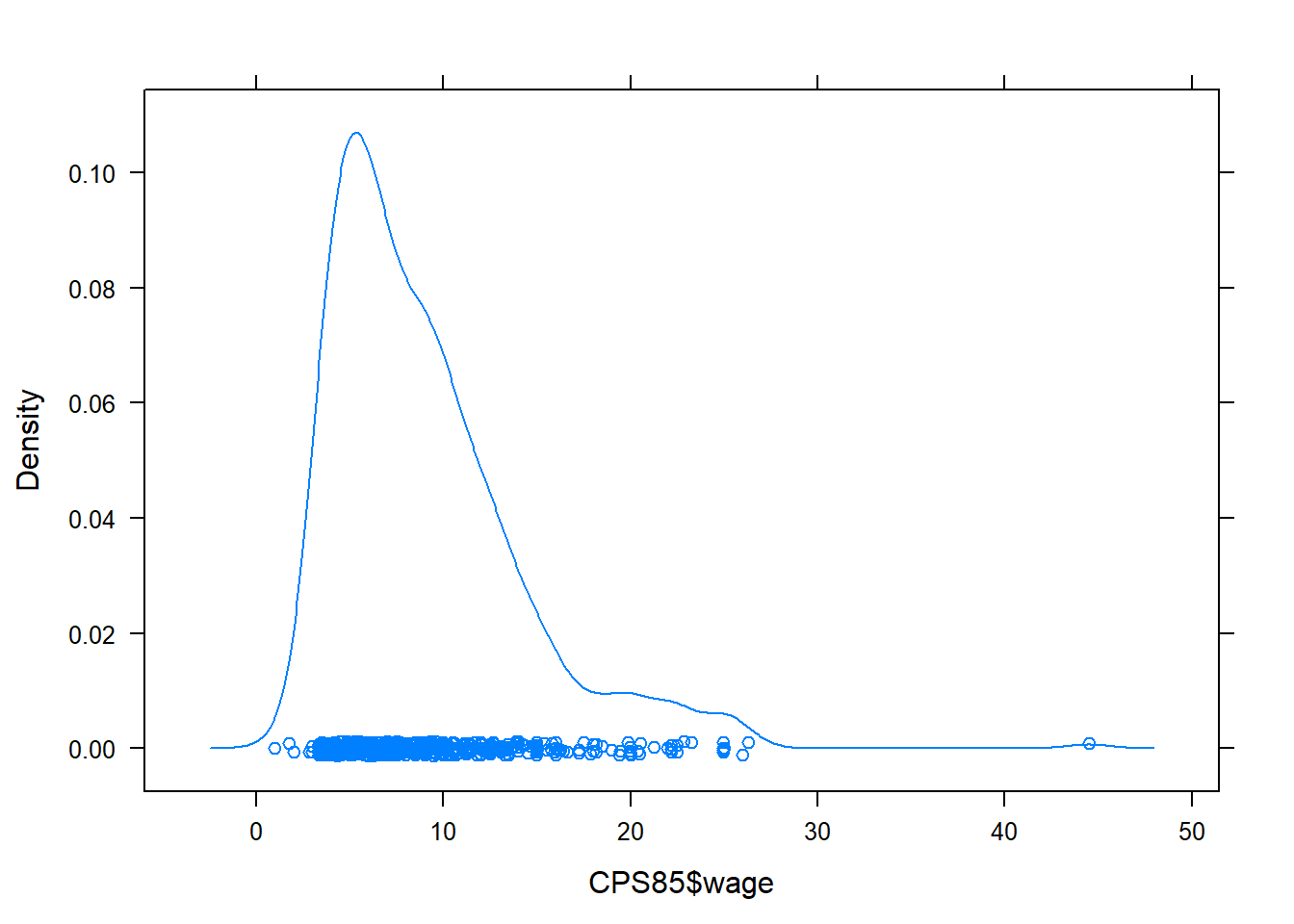
### Exercício Empregue a função rnorm para gerar valores randomicos. Acesse o help(norm). Mas o seu formato geral é:
rnorm( n, valor médio, desvio padrão)gere 4 séries com 100 valores aleatórios com média 50 e desvio padrão 10, 50, 20 e 5 respectivamente. Em seguida plot os gráficos de densidade e compare.
par(mfrow=c(2,2))
plot(density(rnorm(100,50,10)),xlim=c(0,100),main='plot A')
plot(density(rnorm(100,50,50)),xlim=c(0,100),main='plot B')
plot(density(rnorm(100,50,20)),xlim=c(0,100),main='plot C')
plot(density(rnorm(100,50,5)),xlim=c(0,100),main='plot D')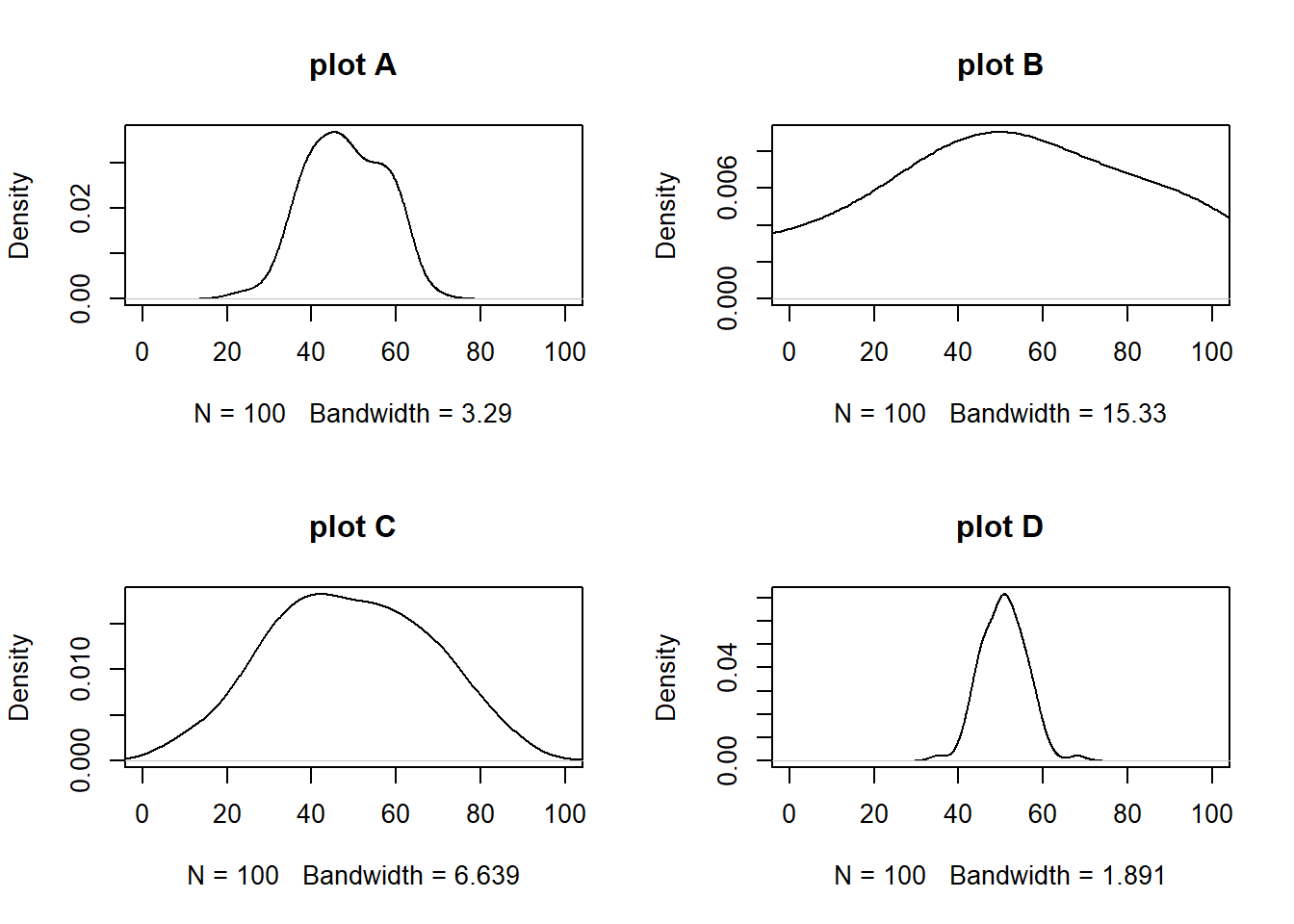
4.8.8 Exercício RESOLVIDO.
Repita o exercício anterior somente para as séries de desvio padrão 10 e 20, mas compare também os histogramas produzidos. Compare os resultados.
par(mfrow=c(2,2))
hist(rnorm(100,50,10),xlim=c(0,100),main='hist A')
plot(density(rnorm(100,50,10)),xlim=c(0,100),main='density A')
hist(rnorm(100,50,20),xlim=c(0,100),main='hist B')
plot(density(rnorm(100,50,20)),xlim=c(0,100),main='density B')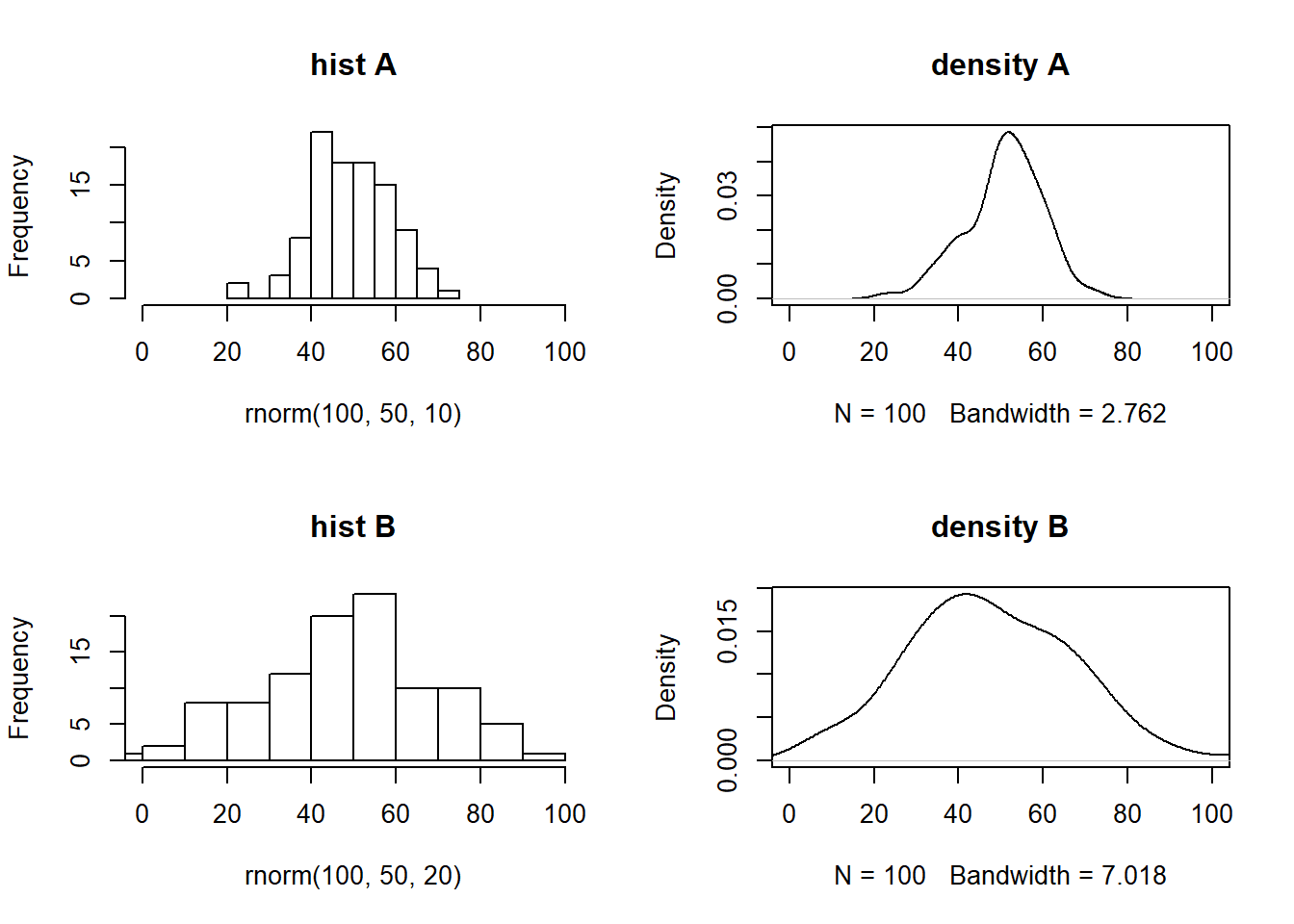
### Exercício Considere a base.
df = read.csv('http://meusite.mackenzie.br/rogerio/TIC/mystocksn.csv')
head(df)## data IBOV VALE3 PETR4 DOLAR
## 1 2020-01-02 118573 13.45 16.27 4.0163
## 2 2020-01-03 117707 13.29 15.99 4.0234
## 3 2020-01-06 116878 13.14 16.22 4.0570
## 4 2020-01-07 116662 13.23 16.06 4.0604
## 5 2020-01-08 116247 13.22 15.70 4.0662
## 6 2020-01-09 115947 12.99 15.75 4.06284.8.9 Exercício
Por quê o gráfico abaixo não exibe os quartis de cada data?
boxplot(DOLAR ~ data, data=df)