Chapter 8 Modelos NAO Supervisionados I
Clusterização é uma tarefa de análise de dados, assim como Classificação, e Regressão, podendo ser empregados vários modelos para se obter a clusterização, como o Kmeans (que veremos aqui), métodos hierárquicos, dbscan etc.
Diferentemente dos modelos anteriores a Clusterização em geral emprega modelos Não Supervisionados.
- APRENDIZADO SUPERVISIONADO
Tarefa: Regressão > Modelo: Linear, Polinomial, Exponencial etc.
Tarefa: Classificação > Modelo: Knn, Árvore de Decisão, Regressão Logística, Redes Neurais etc.
- APRENDIZADO NÃO SUPERVISIONADO
Tarefa: Clusterização > Modelo: Kmeans, Hierárquico,
dbscan
8.1 Aprendizado Não Supervisionado
Diferentemente do Aprendizado Supervisionado, no Aprendizado não Supervisionado não há um Conjunto de Treinamento, e portanto não haverá também um Conjunto de Testes.
O aprendizado feito sobre os dados, capturando algum padrão dos dados, mas sem uma resposta, como um valor ou classe, como você encontrou no Aprendizado Supervisionado. Neste sentido dizemos que o Aprendizado não Supervisionado é mais Analítico que Preditivo.
df = data.frame(matrix(rnorm(300),150,2))
df[1:50,1] = df[1:50,1] + 5; df[1:50,2] = df[1:50,2] + 5
df[51:100,1] = df[51:100,1] - 5; df[51:100,2] = df[51:100,2] + 2
plot(df)
8.2 CUIDADO: Clusterização \(\not=\) Classificação
Um erro comum é confundirmos Clusterização com Classificação.
Suponha por exemplo um conjunto de dados de Empréstimos onde eles são classificados entre Tx Padrão e Tx Especial (juros mais baixos). Essa é a classificação dos dados. Mas, se você buscar com alguma técnica "grupos de Empréstimos" que guardem semelhanças entre si, talvez você encontre grupos que exibem um outra relação dos dados completamente diferente de Tx Padrão e Tx Especial. Por exemplo, grupos de Empréstimos para Bens de Consumo para Jovens, Empréstimos para Capital de Giro e Outros, em todos eles havendo seus percentuais de Tx Padrão e Tx Especial.
Você ainda não vai empregar essa informação para predizer novos casos, mas talvez tomar decisões sobre esses grupos, como fazer uma campanha para educação de Jovens sobre o Empréstimo Consciente ou uma redução das Taxas para atrair mais Empréstimos de Capital de Giro.
8.3 Kmédias
O Kmédias sistematiza a forma que você 'observou' diferentes grupos de dados em nosso exemplo inicial.
É um algoritmo que busca de forma iterativa (aproximações sucessivas) minimizar dois objetivos:
\[ min_{c} J_{in} = \sum_{i,k} || x_i - c_k ||^2 \] \[ max_{c} J_{out} = \sum_{i,k} || c_i - c_k ||^2 \]
Minimizar as distâncias intragrupos e maximizar as distâncias entre grupos.
* Aqui empregaremos unicamente a função distância Euclidiana embora outras funções distância possam ser empregadas.
8.4 Algoritmo Kmeans
1. Seleciona k pontos aleatoriamente como centros de cluster
2. Atribui elementos ao centro de cluster mais próximo de acordo com alguma função distância (euclidiana, por exemplo)
3. Calcula o novo centróide a partir da média de todos os elementos em cada cluster
4. Repite as etapas 2 e 3 até que os mesmos pontos sejam atribuídos a cada cluster em rodadas consecutivas
Veja o exemplo abaixo em uma dimensão.
df = data.frame(age = c(15,15,16,19,19,20,20,21,22,28,35,40,41,42,43,44,60,61,65))
df## age
## 1 15
## 2 15
## 3 16
## 4 19
## 5 19
## 6 20
## 7 20
## 8 21
## 9 22
## 10 28
## 11 35
## 12 40
## 13 41
## 14 42
## 15 43
## 16 44
## 17 60
## 18 61
## 19 65kmeans(df,2)## K-means clustering with 2 clusters of sizes 10, 9
##
## Cluster means:
## age
## 1 19.50000
## 2 47.88889
##
## Clustering vector:
## [1] 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2
##
## Within cluster sum of squares by cluster:
## [1] 134.5000 960.8889
## (between_SS / total_SS = 77.7 %)
##
## Available components:
##
## [1] "cluster" "centers" "totss" "withinss" "tot.withinss"
## [6] "betweenss" "size" "iter" "ifault"8.5 Kmeans em R
# install.packages("factoextra")
# install.packages("cluster")
# install.packages('fpc')
library("cluster")
library("factoextra") # fviz_*## Warning: package 'factoextra' was built under R version 3.5.3## Loading required package: ggplot2## Warning: package 'ggplot2' was built under R version 3.5.3## Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBalibrary('fpc') # plotcluster## Warning: package 'fpc' was built under R version 3.5.3RNGversion("3.5.2")
set.seed(1984)
#
# USAarrests Data
my_data = USArrests
head(my_data)## Murder Assault UrbanPop Rape
## Alabama 13.2 236 58 21.2
## Alaska 10.0 263 48 44.5
## Arizona 8.1 294 80 31.0
## Arkansas 8.8 190 50 19.5
## California 9.0 276 91 40.6
## Colorado 7.9 204 78 38.7nrow(my_data)## [1] 50ncol(my_data)## [1] 4#
# Preparação dos Dados. Clean NA values, Scale Data
my_data = na.omit(my_data)
my_data = data.frame(scale(USArrests))
head(my_data)## Murder Assault UrbanPop Rape
## Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
## Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
## Arizona 0.07163341 1.4788032 0.9989801 1.042878388
## Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
## California 0.27826823 1.2628144 1.7589234 2.067820292
## Colorado 0.02571456 0.3988593 0.8608085 1.864967207#
# Kmeans, 3 grupos
fit = kmeans(my_data, 3, nstart = 25)
print(fit)## K-means clustering with 3 clusters of sizes 13, 17, 20
##
## Cluster means:
## Murder Assault UrbanPop Rape
## 1 -0.9615407 -1.1066010 -0.9301069 -0.9667633
## 2 -0.4469795 -0.3465138 0.4788049 -0.2571398
## 3 1.0049340 1.0138274 0.1975853 0.8469650
##
## Clustering vector:
## Alabama Alaska Arizona Arkansas California
## 3 3 3 2 3
## Colorado Connecticut Delaware Florida Georgia
## 3 2 2 3 3
## Hawaii Idaho Illinois Indiana Iowa
## 2 1 3 2 1
## Kansas Kentucky Louisiana Maine Maryland
## 2 1 3 1 3
## Massachusetts Michigan Minnesota Mississippi Missouri
## 2 3 1 3 3
## Montana Nebraska Nevada New Hampshire New Jersey
## 1 1 3 1 2
## New Mexico New York North Carolina North Dakota Ohio
## 3 3 3 1 2
## Oklahoma Oregon Pennsylvania Rhode Island South Carolina
## 2 2 2 2 3
## South Dakota Tennessee Texas Utah Vermont
## 1 3 3 2 1
## Virginia Washington West Virginia Wisconsin Wyoming
## 2 2 1 1 2
##
## Within cluster sum of squares by cluster:
## [1] 11.95246 19.62285 46.74796
## (between_SS / total_SS = 60.0 %)
##
## Available components:
##
## [1] "cluster" "centers" "totss" "withinss" "tot.withinss"
## [6] "betweenss" "size" "iter" "ifault"#
# Explore alguns resultados...
# "cluster" "centers" "withinss" "betweenss" "size"
print(fit$withinss)## [1] 11.95246 19.62285 46.74796print(fit$cluster)## Alabama Alaska Arizona Arkansas California
## 3 3 3 2 3
## Colorado Connecticut Delaware Florida Georgia
## 3 2 2 3 3
## Hawaii Idaho Illinois Indiana Iowa
## 2 1 3 2 1
## Kansas Kentucky Louisiana Maine Maryland
## 2 1 3 1 3
## Massachusetts Michigan Minnesota Mississippi Missouri
## 2 3 1 3 3
## Montana Nebraska Nevada New Hampshire New Jersey
## 1 1 3 1 2
## New Mexico New York North Carolina North Dakota Ohio
## 3 3 3 1 2
## Oklahoma Oregon Pennsylvania Rhode Island South Carolina
## 2 2 2 2 3
## South Dakota Tennessee Texas Utah Vermont
## 1 3 3 2 1
## Virginia Washington West Virginia Wisconsin Wyoming
## 2 2 1 1 2#
# Veja os grupos formados
my_data = cbind(my_data,as.numeric(fit$cluster))
colnames(my_data)[5] = 'cluster'
print(my_data[my_data$cluster == 2,]) ## Murder Assault UrbanPop Rape cluster
## Arkansas 0.23234938 0.23086801 -1.07359268 -0.18491660 2
## Connecticut -1.03041900 -0.72908214 0.79172279 -1.08174077 2
## Delaware -0.43347395 0.80683810 0.44629400 -0.57994629 2
## Hawaii -0.57123050 -1.49704226 1.20623733 -0.11018125 2
## Indiana -0.13500142 -0.69308401 -0.03730631 -0.02476943 2
## Kansas -0.41051452 -0.66908525 0.03177945 -0.34506377 2
## Massachusetts -0.77786532 -0.26110644 1.34440885 -0.52656390 2
## New Jersey -0.08908257 -0.14111267 1.62075188 -0.25965195 2
## Ohio -0.11204199 -0.60908837 0.65355127 0.01793648 2
## Oklahoma -0.27275797 -0.23710769 0.16995096 -0.13153421 2
## Oregon -0.66306820 -0.14111267 0.10086521 0.86137826 2
## Pennsylvania -0.34163624 -0.77707965 0.44629400 -0.67603460 2
## Rhode Island -1.00745957 0.03887798 1.48258036 -1.38068216 2
## Utah -1.05337842 -0.60908837 0.99898006 0.17808366 2
## Virginia 0.16347111 -0.17711080 -0.17547783 -0.05679886 2
## Washington -0.86970302 -0.30910395 0.51537975 0.53040744 2
## Wyoming -0.22683912 -0.11711392 -0.38273510 -0.60129925 28.6 Visualizando os grupos
#
# Visualização Gráfica
plotcluster(my_data, fit$cluster)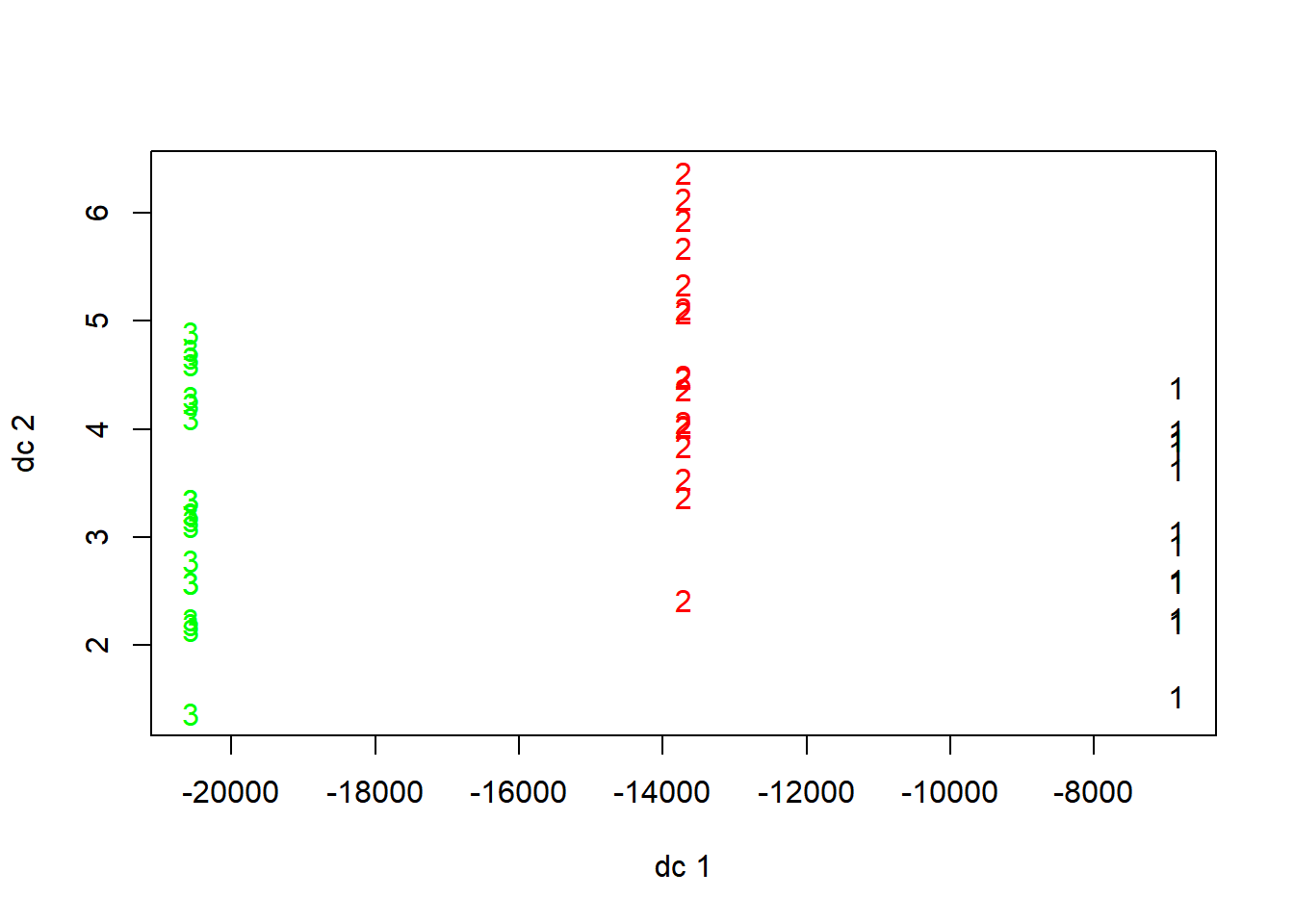
# ou...
par(mfrow=c(1, 1))
clusplot(my_data, fit$cluster, color=TRUE, shade=TRUE, labels=2, lines=0)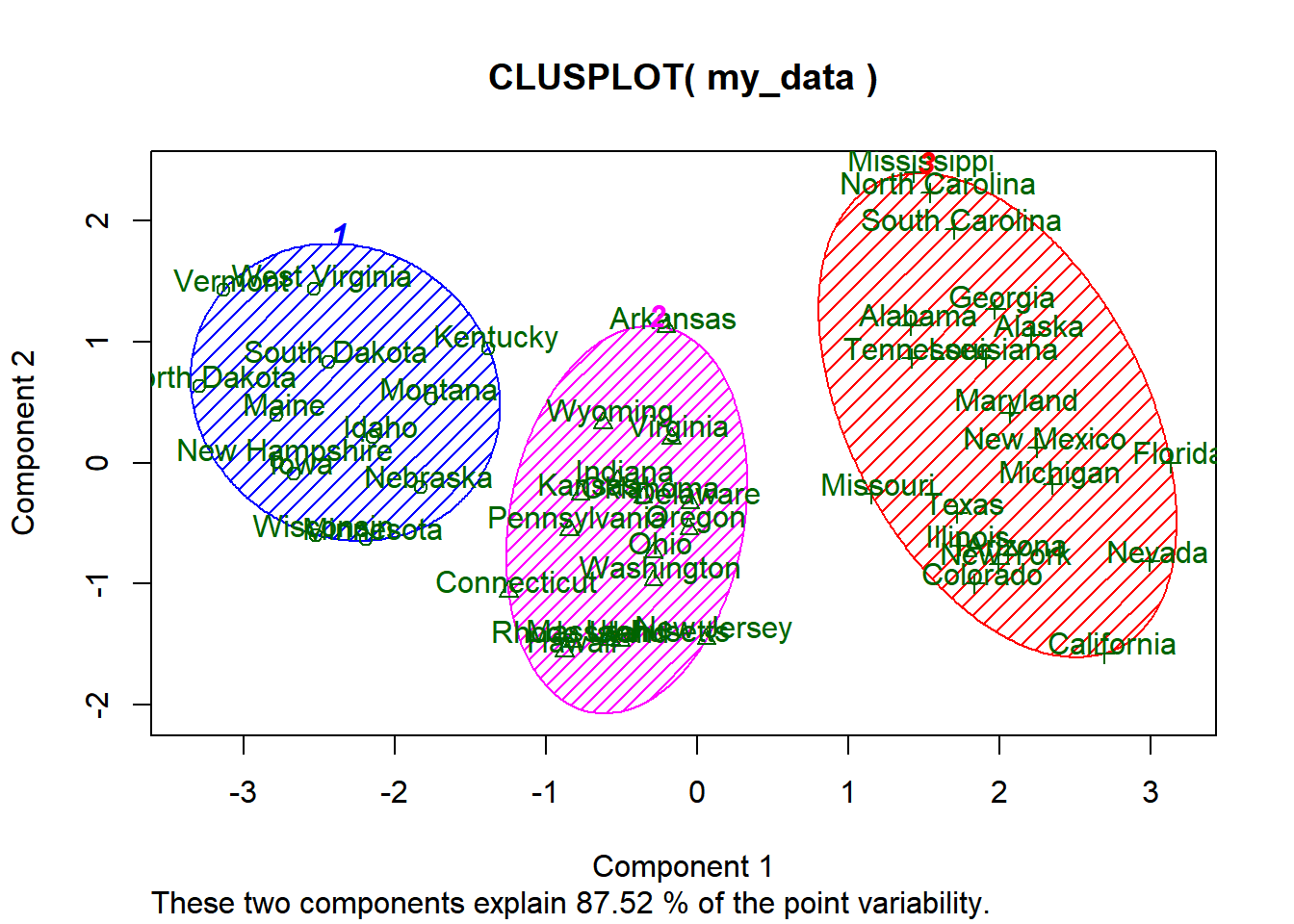
8.7 Elbow Rule
wss = 0
bss = 0
for (i in 1:10) wss[i] = sum(kmeans(my_data,i, nstart=25)$withinss)
for (i in 1:10) bss[i] = sum(kmeans(my_data,i, nstart=25)$betweenss)
par(mfrow=c(1,2))
plot(1:10, wss, type="b", xlab="Number of Clusters", ylab="Within groups sum of squares")
abline(v=3,col="red")
plot(1:10, bss, type="b", xlab="Number of Clusters", ylab="Betweenss groups sum of squares")
abline(v=3,col="red")
Outra métrica útil é verificar o tamanho dos grupos, existindo ainda métricas sofisticadas como o silhouette.
par(mfrow=c(2,2))
for (i in 3:6){
fit <- kmeans(my_data,i, nstart=25)
main_ = paste("Size groups for k=", i)
barplot(fit$size, main = main_ )
} 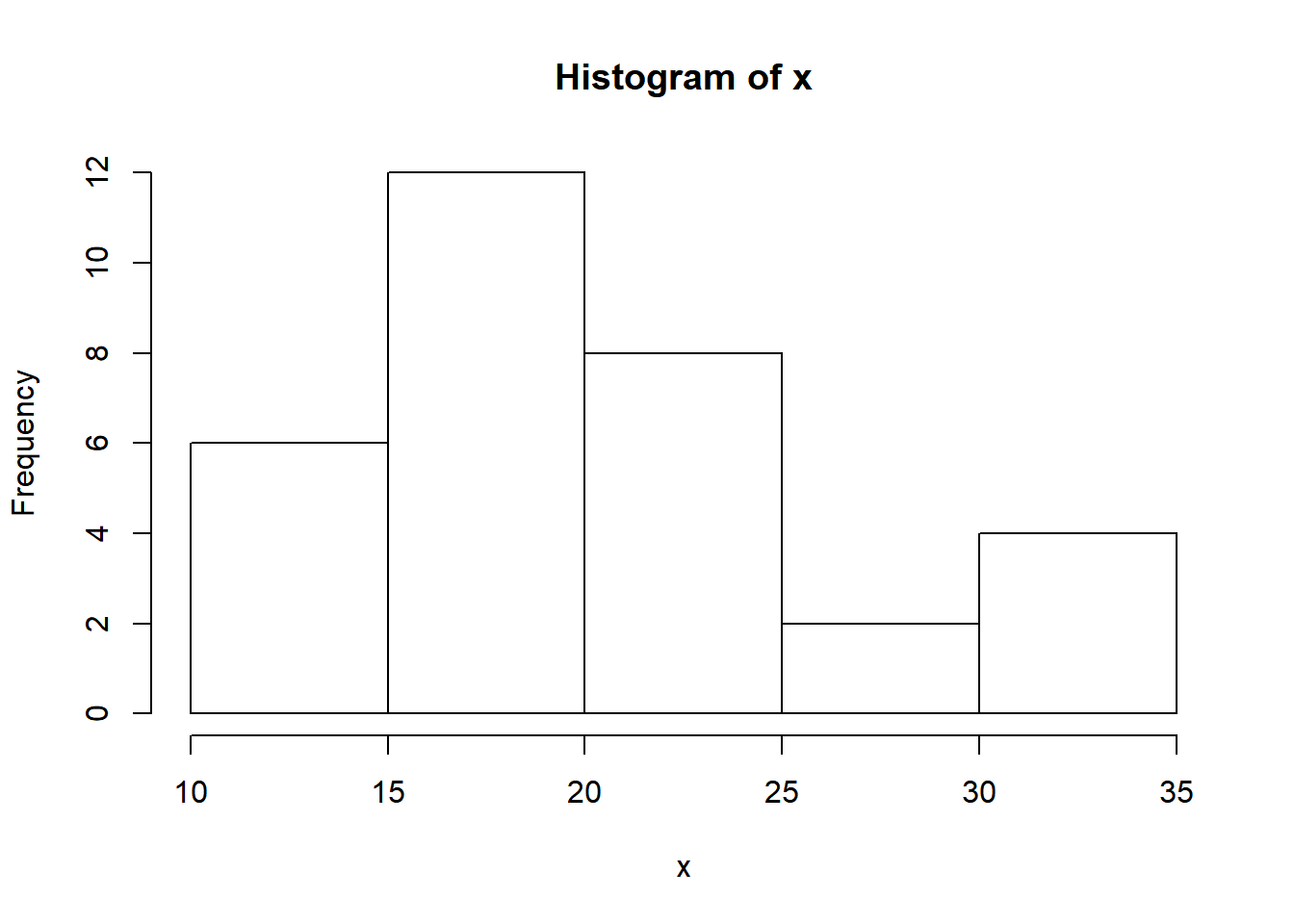
8.8 Caracterizando os Grupos
Esses grupos, diferentemente de um processo de classificação (Tx Padrão, Tx Especial) não são caracterizados por um rótulo. Mas você pode explorar esses grupos, por exemplo verificando os valores médios, buscando características comuns para que vocês rotula-los e, portanto, caracteriza-los melhor.
No nosso exemplo anterior, você só pode identificar que existem grupos de Empréstimos para Bens de Consumo para Jovens e Empréstimos para Capital de Giro e Outros, observando por exemplo os produtos, finalidade do empréstimo e idade média dos clientes de cada grupo.
#
# Caracterizando os grupos
par(mfrow=c(1, 3))
for (i in 1:3){
main_ = paste("Group =", i)
barplot(sapply(my_data[my_data$cluster==i,-5],mean),main=main_)
}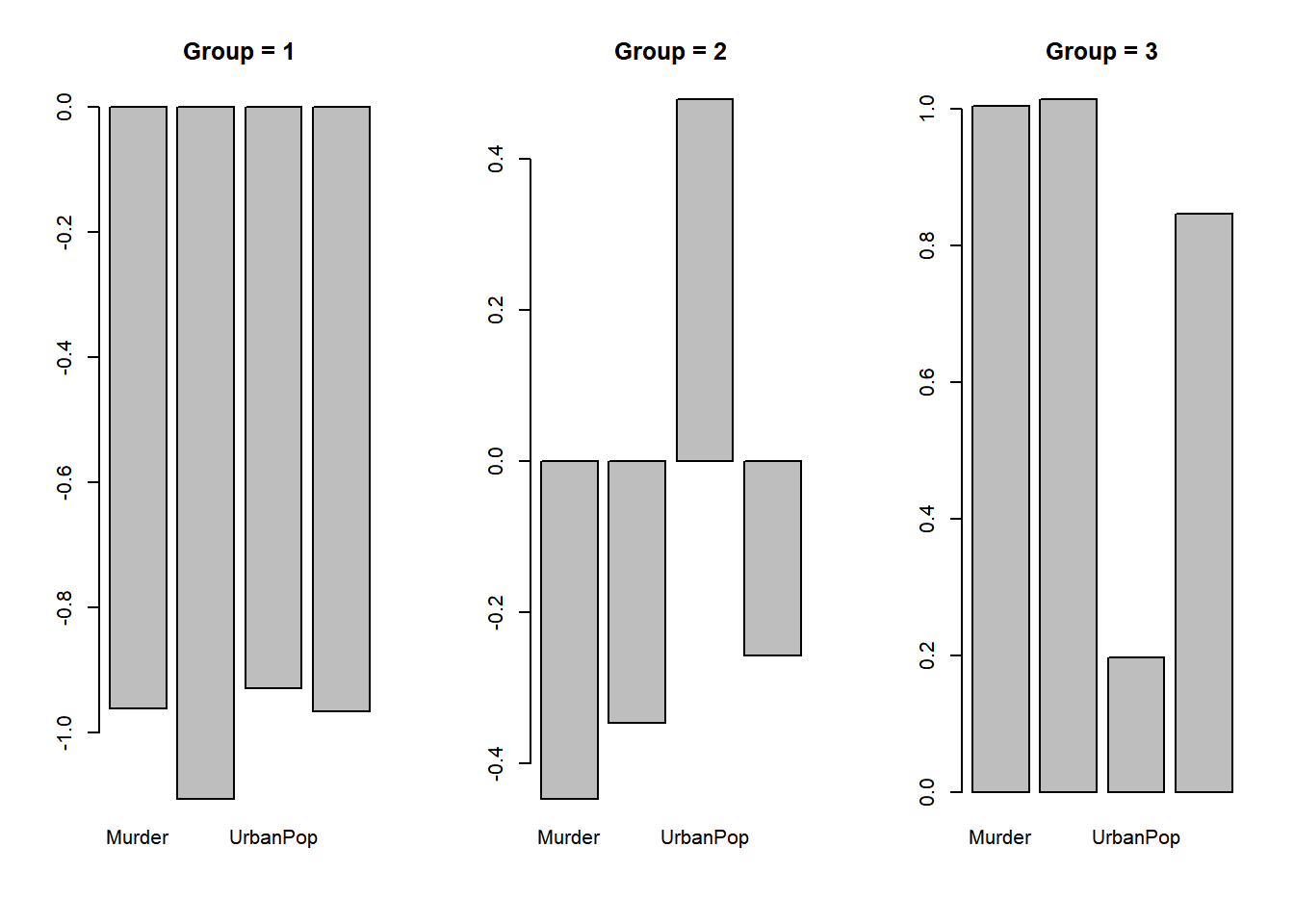
# 1 = Urbanizado com Baixa Violência
# 2 = Rural com Baixa Violência
# 3 = Urbanizado com Alta Violência8.9 Exercícios.
Empregue o dataset abaixo para fazer uma clusterização kmédias seguindo o questionário do Moodle. Para clusterização, desconsidere os atributos Channel e Region. Estamos interessados em seguimentar os fornecedores por produtos!
Não esqueça de empregar o RNGVersion e o seed para que você possa responder os testes.
RNGversion('3.5.2')
set.seed(1984)
mydata_ = read.csv('http://meusite.mackenzie.br/rogerio/Wholesale customers data.csv',header=T)
head(mydata_)## Channel Region Fresh Milk Grocery Frozen Detergents_Paper Delicassen
## 1 2 3 12669 9656 7561 214 2674 1338
## 2 2 3 7057 9810 9568 1762 3293 1776
## 3 2 3 6353 8808 7684 2405 3516 7844
## 4 1 3 13265 1196 4221 6404 507 1788
## 5 2 3 22615 5410 7198 3915 1777 5185
## 6 2 3 9413 8259 5126 666 1795 1451