Chapter 9 Modelos NAO Supervisionados II
9.1 Clustering Hierárquico
Clustering hierárquico (ou análise de cluster hierárquico) é um método de análise de cluster que busca construir uma hierarquia de clusters. Existem duas estratégias normalmente empregadas:
Aglomerativo: Esta é uma abordagem "de baixo para cima", cada observação começa em seu próprio agrupamento, e pares de agrupamentos são organizados a medida que sobe a hierarquia.
Divisivo: Esta é uma abordagem "de cima para baixo", todas as observações começam em um cluster, e as divisões são realizadas recursivamente à medida que se desce na hierarquia dos dados.
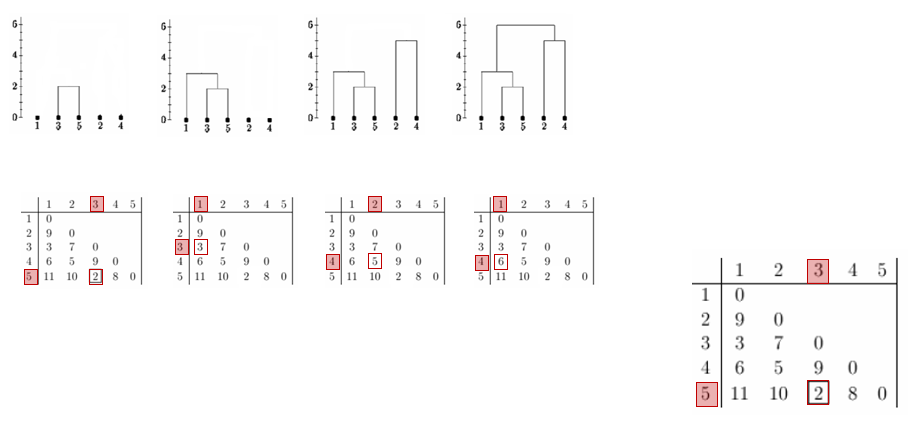
Os resultados do agrupamento hierárquico podem ser então apresentados em um dendrograma.
9.2 Funções Distância
Existem várias funções distância que podem ser aplicadas, não só aqui mas também nos modelos anteriores que estudamos (knn, kmeans etc.). A distância euclidiana é a mais aplicada, mas algumas algumas encontram maior uso em contextos específicos como a distância de Hamming para dados binários ou a distância coseno para análise de dados de documentos.
Uma função é uma função distância se atende a 4 propriedades:
\[ d(x,y) \ge 0\] \[ d(x,x) = 0\] \[ d(x,y) = d(y,x)\] \[ d(x,y) \le d(x,z) + d(z,y)\]
9.3 Algumas funções distância empregadas em Ciência de Dados
Veja aqui algumas funções distância:
Distância euclidiana \[{\| ab \| _ {2} = {\sqrt {\sum _ {i} (a_ {i} -b_ {i}) ^ {2}}}} \]
Distância euclidiana quadrada \[{\| ab \| _ {2} ^ {2} = \sum _ {i} (a_ {i} -b_ {i}) ^ {2}} \]
Distância de Manhattan \[{\| ab \| _ {1} = \sum _ {i} | a_ {i} -b_ {i} |}\]
Distância máxima \[{\| ab \| _ {\infty} = \max _ {i} | a_ {i} -b_ {i} |}\]
Distância de Mahalanobis \[{{\sqrt {(ab) ^ {\top} S ^ {- 1} (ab)}}}\] onde S é a matriz de covariância
9.3.0.1 Distância de Hamming para Strings
def hamming_distance(s1, s2):
assert len(s1) == len(s2)
return sum(ch1 != ch2 for ch1, ch2 in zip(s1, s2))9.3.0.2 Distância Cosseno
Aplicada para problemas em geral de busca e análise de documentos com representação vetorial (bow, tf-idf etc.).
\[ A.B = \|A\| \|B\| cos(\theta)\]
Então definimos a similaridade de dois vetores como:
\[ S(A,B) = cos(\theta) = \frac{A.B}{\|A\| \|B\|} \]
E a distância:
\[ d(A,B) = 1 - S(A,B)\]
9.4 Definindo os Clusters
Construído o Dendograma, a partir da matriz de distância dos elementos, a definição dos Clusters pode ser feita estabelecendo-se um ponto de corte no dendograma que é a distância máxima que os elementos terão dentro de um agrupamento.
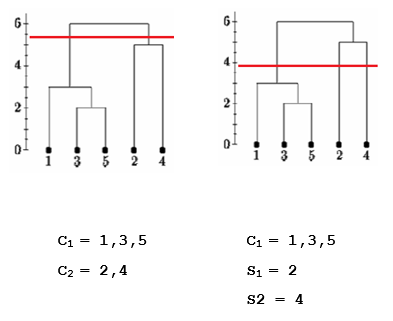
A definição do melhor número de agrupamentos segue algumas métricas e técnicas á exemplo do que vimos no k-Médias.
9.5 Linkage
A função distância está bem definida para distância de dois elementos. Mas ainda não definimos a distância de um elemento a um grupo. O critério de ligação determina a distância entre conjuntos de observações e ou entre conjuntos e um elemento.
Alguns dos critérios de ligação comumente empregados são:
- Complete linkage
\[d(A,B) = \{\max \, d (a, b): a \in A, \, b \in B \, \}\]
- Single linkage
\[d(A,B) = \{\min \, d (a, b): a \in A, \, b \in B \, \}\]
- Average linkage
\[d(A,B) = {\displaystyle {\frac {1} {| A | \cdot | B |}} \sum _ {a \in A} \sum _ {b \in B} d (a, b)} \]
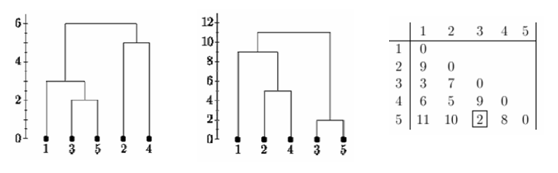
Importante notar que o tipo de linkage empregado altera a formação dos agrupamentos além de ter impacto sobre o desempenho do processamento (ver seção opcional abaixo).
Abaixo, diferentes formações para singlee complete linkage.
9.6 Complexidade * (um tópico opcional avançado)
O algoritmo padrão para agrupamento aglomerativo hierárquico tem uma complexidade de tempo de O(n3) e requer Ω(n2) de Memória, o que o torna muito lento até mesmo para conjuntos de dados de tamanhos médios. No entanto, para alguns casos especiais, métodos aglomerativos eficientes ideais (de complexidade O(n2) são conhecidos Single Linkage para ligação única e Complete Linkage para agrupamento de ligação completa. Com um heap, o tempo de execução do caso geral pode ser reduzido para O(n2 logn) , uma melhoria no limite mencionado de O(n3) , ao custo de aumentar ainda mais o requisitos de memória. Em muitos casos, a sobrecarga de memória dessa abordagem é muito grande para torná-la utilizável na prática.
Exceto para o caso especial de ligação única, nenhum dos algoritmos (exceto pesquisa exaustiva em O(2n) pode ser garantido para encontrar a solução ideal.
O agrupamento divisivo com uma pesquisa exaustiva é O(2n) , mas é comum usar heurísticas mais rápidas para escolher divisões, como k-médias.
9.7 Comparando os Métodos
Abaixo uma exploração de como os métodos de Clusterização Partitivo (K-médias), Hierárquico e DBScan podem diferenciar. Ver: https://scikit-learn.org/stable/modules/clustering.html
9.8 Cluster Hierárquico em R
A clusterização segue os mesmos passos que apresentamos: a construção de uma matriz de distâncias, seguido da definição de um ponto de corte. Veja o exemplo de clusterização de USArrests.
library("cluster")
library('fpc') # plotcluster## Warning: package 'fpc' was built under R version 3.5.3#
#
# USAarrests Data
my_data = USArrests
head(my_data)## Murder Assault UrbanPop Rape
## Alabama 13.2 236 58 21.2
## Alaska 10.0 263 48 44.5
## Arizona 8.1 294 80 31.0
## Arkansas 8.8 190 50 19.5
## California 9.0 276 91 40.6
## Colorado 7.9 204 78 38.7nrow(my_data)## [1] 50ncol(my_data)## [1] 4#
#
# Preparação dos Dados. Clean NA values, Scale Data
my_data = na.omit(my_data)
my_data = data.frame(scale(USArrests))
head(my_data)## Murder Assault UrbanPop Rape
## Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
## Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
## Arizona 0.07163341 1.4788032 0.9989801 1.042878388
## Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
## California 0.27826823 1.2628144 1.7589234 2.067820292
## Colorado 0.02571456 0.3988593 0.8608085 1.864967207#
#
# Cálculo da Matriz de Distâncias
d = dist(as.matrix(my_data),method = 'euclidean')
#
#
# Construção do Dendograma (Modelo)
fit = hclust(d, method = "complete")
# fit = hclust(d, method = "single")
# fit = hclust(d, method = "average")
print(fit)##
## Call:
## hclust(d = d, method = "complete")
##
## Cluster method : complete
## Distance : euclidean
## Number of objects: 50#
#
# plot Dendograma e Corte
par(mfrow=c(1, 1))
plot(fit)
rect.hclust(fit, k = 3, border = "red")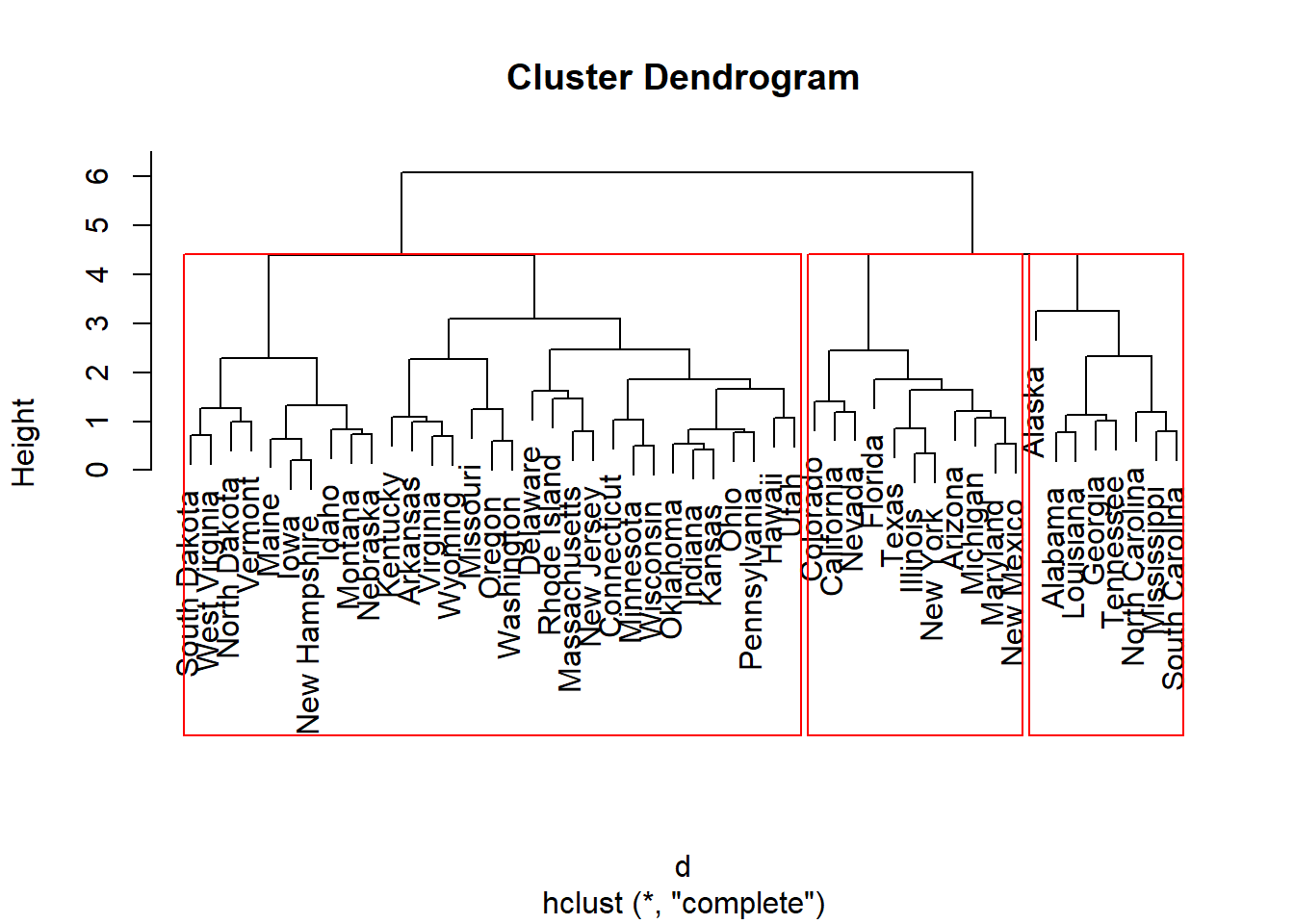
#
#
# Clusters ocm um corte em 3 clusters
groups = cutree(fit, k=3)
#
#
# Veja os grupos formados
my_data = cbind(my_data,as.numeric(groups))
colnames(my_data)[5] = 'cluster'
print(my_data[my_data$cluster == 2,]) ## Murder Assault UrbanPop Rape cluster
## Arizona 0.07163341 1.4788032 0.9989801 1.0428784 2
## California 0.27826823 1.2628144 1.7589234 2.0678203 2
## Colorado 0.02571456 0.3988593 0.8608085 1.8649672 2
## Florida 1.74767144 1.9707777 0.9989801 1.1389667 2
## Illinois 0.59970018 0.9388312 1.2062373 0.2955249 2
## Maryland 0.80633501 1.5507995 0.1008652 0.7012311 2
## Michigan 0.99001041 1.0108275 0.5844655 1.4806140 2
## Nevada 1.01296983 0.9748294 1.0680658 2.6443501 2
## New Mexico 0.82929443 1.3708088 0.3081225 1.1603196 2
## New York 0.76041616 0.9988281 1.4134946 0.5197310 2
## Texas 1.12776696 0.3628612 0.9989801 0.4556721 2#
#
# Visualização Gráfica
par(mfrow=c(1, 1))
plotcluster(my_data, my_data$cluster)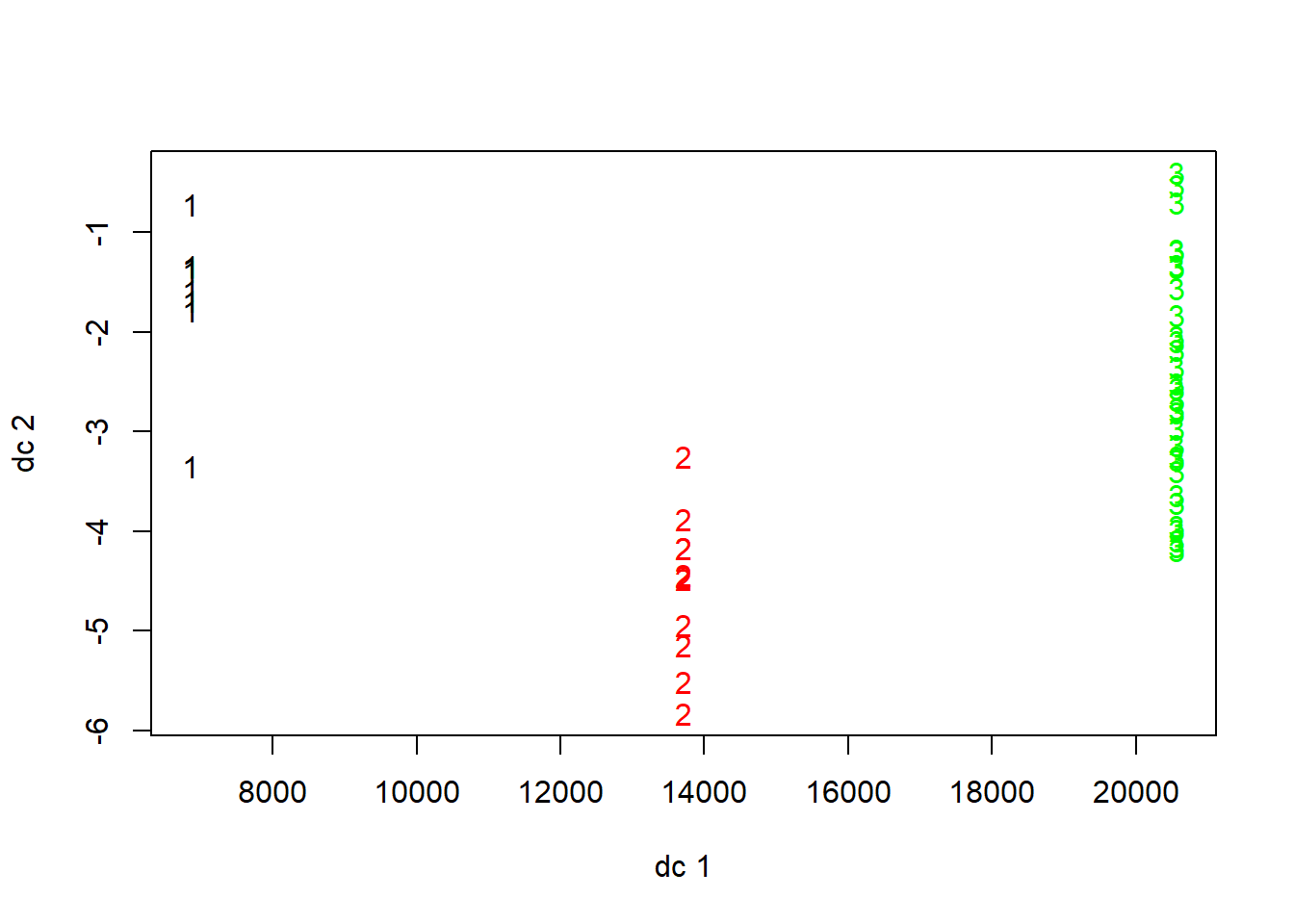
# ou...
par(mfrow=c(1, 1))
clusplot(my_data, groups, color=TRUE, shade=TRUE, labels=2, lines=0)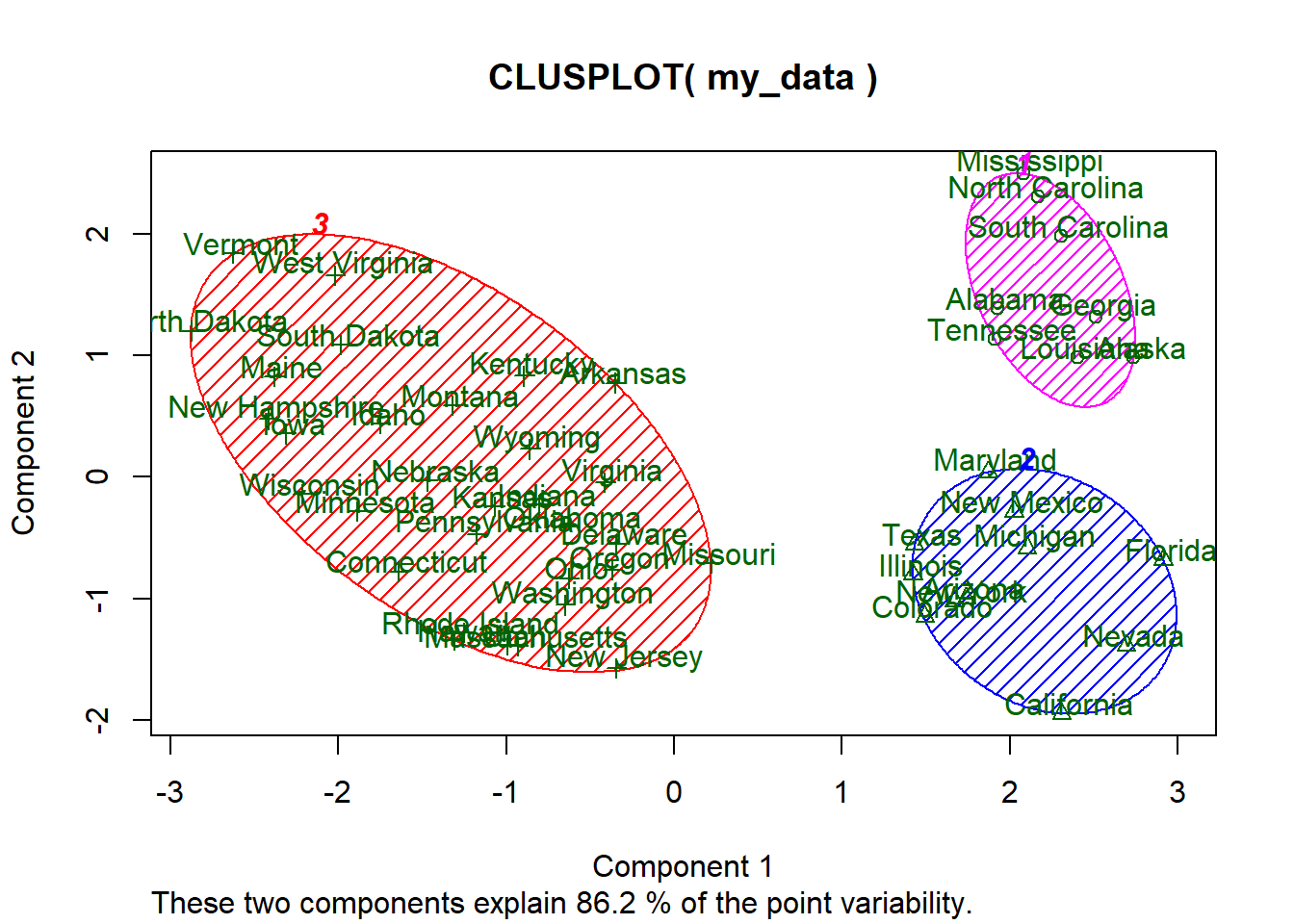
9.9 Caracterização dos dados
A caracterização dos dados segue os mesmos princípios de caracterização de clusters kmeans.
#
#
# Caracterizando os grupos pelos valores médios
par(mfrow=c(1, 3))
for (i in 1:3){
main_ = paste("Group =", i)
barplot(sapply(my_data[my_data$cluster==i,c(1:4)],mean),main=main_)
}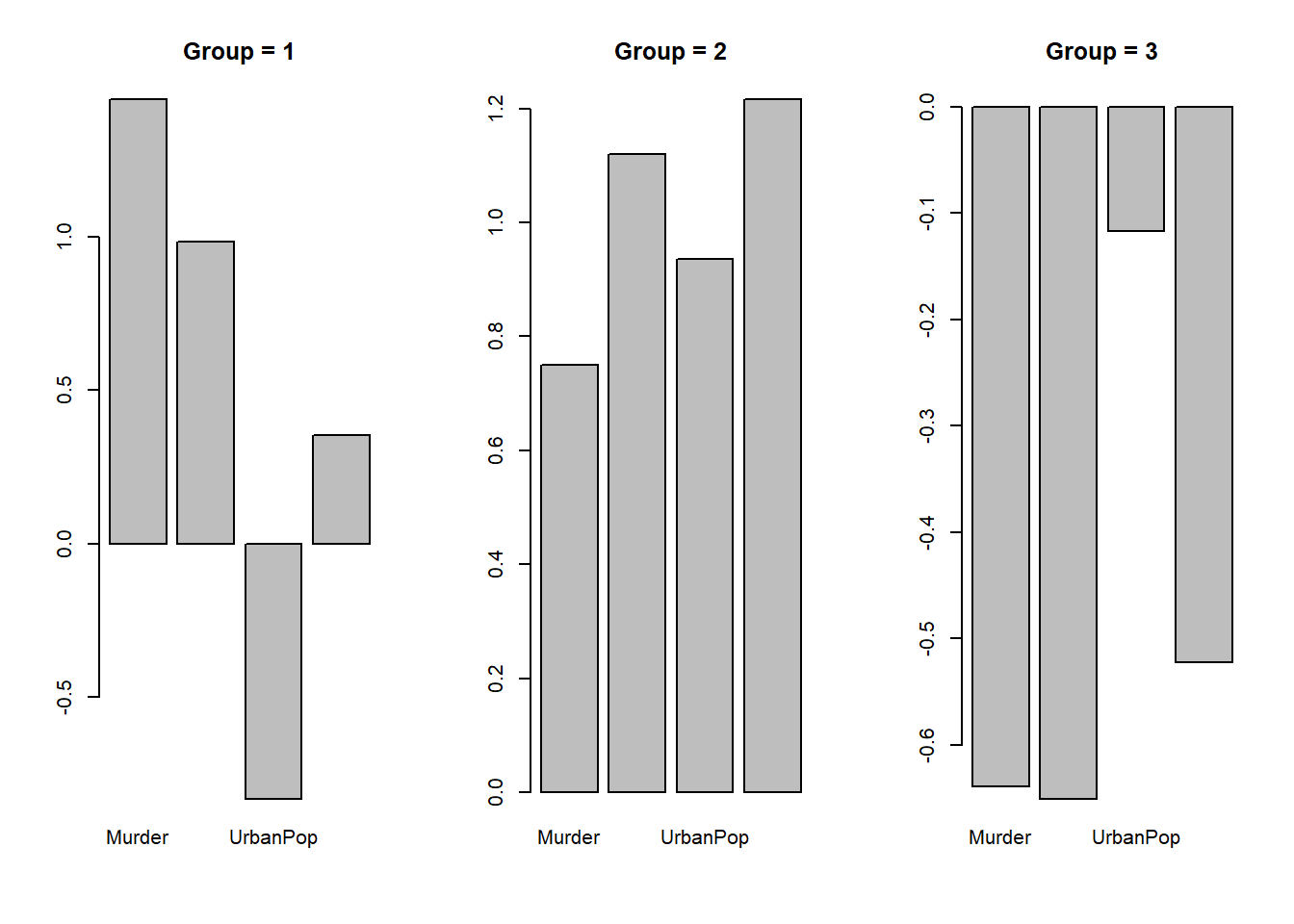
# 1 = Urbanizado com Baixa Violência
# 2 = Rural com Baixa Violência
# 3 = Urbanizado com Alta Violência9.10 Silhouette, métrica
Podemos também empregar outras métricas para definirmos o melhor número de clusters. A mais comum é o emprego do Silhouette:
https://en.wikipedia.org/wiki/Silhouette_(clustering)
#
#
# Silhouette, mais uma métrica para definição do número de Clusters
#
# O número de Clusters pode, entretanto, seguir outros critérios como critérios do problema/negócio
set.seed(1984)
for (i in 2:10){
d = dist(as.matrix(my_data),method = 'euclidean')
fit = hclust(d, method = "complete")
groups = cutree(fit, k=i)
ss = silhouette(groups, d)
# plot(ss)
cat('Média de Silhouette para ', i , ' clusters = ', mean(ss[,3]) , '\n')
} ## Média de Silhouette para 2 clusters = 0.4544212
## Média de Silhouette para 3 clusters = 0.429055
## Média de Silhouette para 4 clusters = 0.344597
## Média de Silhouette para 5 clusters = 0.3457801
## Média de Silhouette para 6 clusters = 0.2921377
## Média de Silhouette para 7 clusters = 0.2789948
## Média de Silhouette para 8 clusters = 0.2578745
## Média de Silhouette para 9 clusters = 0.2477031
## Média de Silhouette para 10 clusters = 0.2121965# plot best...
for (i in 2){
d = dist(as.matrix(my_data),method = 'euclidean')
fit = hclust(d, method = "complete")
groups = cutree(fit, k=i)
ss = silhouette(groups, d)
plot(ss)
cat('Média de Silhouette para ', i , ' clusters = ', mean(ss[,3]) , '\n')
} 
## Média de Silhouette para 2 clusters = 0.45442129.11 Exercício.
Empregue a Clusterização Hierárquica para analisar o seguinte conjunto de dados médicos.
medical = read.csv("http://meusite.mackenzie.br//rogerio//ML//MedicalDataKarimNahasKaggle.csv",header=T)
head(medical)## id gender dob zipcode employment_status education
## 1 Amelia Nixon female 1944-03-09 89136 retired bachelors
## 2 Clara Hicks female 1966-07-02 94105 employed phd/md
## 3 Mason Brown male 1981-05-31 89127 employed masters
## 4 Michael Rice male 1945-02-13 44101 retired bachelors
## 5 Eleanor Ritter female 1939-09-03 89136 retired masters
## 6 Sofia Wise female 1956-10-16 94105 unemployed highschool
## marital_status children ancestry avg_commute daily_internet_use
## 1 married 1 Portugal 13.38 2.53
## 2 married 4 Sweden 15.16 6.77
## 3 married 2 Germany 23.60 3.63
## 4 married 2 Denmark 19.61 5.00
## 5 married 3 Austria 36.55 7.75
## 6 married 2 Austria 48.68 3.34
## available_vehicles military_service disease
## 1 2 no hypertension
## 2 2 no endometriosis
## 3 1 no prostate cancer
## 4 3 no multiple sclerosis
## 5 1 no skin cancer
## 6 0 no Alzheimer's disease- Explore o conjunto de dados
- Elimine os atributos
idediseasena clusterização - Proceda as seguintes transformações dos dados:
Converta o atributo de data para somente o número de anos ´´´{r} # medical$dob = substr(dob,1,4) # para modificar date to year´ ´´´
NÃO FAÇA OS SCALE DOS DADOS. Ver próximo exercício.
Faça o hot encode (dummy encode) de todos os atributos categóricos
- Encontre o melhor número de clusters pelo critério silhouette para a distância euclidiana e linkage complete
- Faça a clusterização pelo número de cluster obtido no item anterior (distância euclidiana e linkage complete)
- Responda as perguntas no Moodle
9.12 Exercício. Scale
Verifique o impacto no modelo com o scale dos dados após o hot encode.
9.13 Exercício. Disease
Verifique o impacto no modelo com o acréscimo do atributo classe disease.