Chapter 7 Regressao Linear
Um modelo linear aproxima o valor de variável objetivo \(Y\) a partir de uma combinação linear das variáveis preditoras \(X\).
\[ \widehat Y = a_0 + a_{1} X_{1} + a_{2} X_{2} + ... + a_{n} X_{n} \]
A cada variável preditora corresponde um coeficiente \(a_n\), havendo um coeficiente independente que corresponte ao valor de \(\widehat Y\) para \(X=0\) (intercept).
7.1 Obtendo os Coeficiente \(a_n\), Método dos Mínimos Quadrados
Os coeficientes \(a_n\) podem ser obtidos minimizando-se a soma da distância entre os valores reais \(Y\) e os valores estimados \(\widehat Y\).
Para uma única variável \(X\), podemos escrever:
\[min \sum d(Y, \widehat Y) = \]
\[ min \sum (y_i - \widehat y_i )^2 = \]
\[ min \sum (y_i - a_0 - a_i x_i )^2 \]
Esta é uma função convexa e os pontos de mínimo com relação aos valores coeficientes podem ser obtidos derivando-se a função. O resultado será:
\[a_1 = \frac{COV(x,y)}{VAR(x)} \]
\[a_0 = \bar y - a_1 \bar x \]
Para mais detalhes veja: 1. https://en.wikipedia.org/wiki/Regression_analysis 2. https://pt.wikipedia.org/wiki/M%C3%A9todo_dos_m%C3%ADnimos_quadrados
7.2 Coeficiente de Determinação, \(R^2\)
O Coeficiente de Determinação, Coeficiente de Correlação, ou ainda \(R-\)Square é uma medida de \([0,1]\) que indica o quanto um modelo linear explica um conjunto de dados. Quanto mais próximo de 1, mais os dados se aproximam de um modelo linear.
\[ R^2 = 1 - \frac{SS_e}{SS_{total}} \]
onde
\[SS_e = \sum (y_i - \widehat y_i )^2 \] é o (erro) resíduo e,
\[SS_{total} = \sum (y_i - \bar y )^2 \]
o erro total.
Para mais detalhes veja: 1. https://en.wikipedia.org/wiki/Coefficient_of_determination
7.3 \(p-value\) dos Coeficientes
Outra medida importante sobre o p-value dos coeficientes. Assumindo a hipótese nula do coeficiente ser igual a zero, buscamos coeficientes cujo p-value rejeitem a hipótese nula.
\[ H_0: a_i = 0 \] \[ H_a: a_i \neq 0 \]
7.4 Intervalo de Confiança dos Coeficientes
O Intervalo de Confiança dos Coeficientes possui duas definições equivalentes:
- O intervalo é o conjunto de valores para os quais um teste de hipótese para o nível de 5% não pode ser rejeitado.
- O intervalo tem uma probabilidade de 95% de conter o verdadeiro valor de \(a_i\) ou ainda, em 95% de todas as amostras que poderiam ser coletadas, o intervalo de confiança cobrirá o valor real de \(a_i\).
Para mais detalhes dos intervalos de confiança e p-value, veja:
7.5 Aplicação
Vamos considerar os valores de faithful.
head(faithful)## eruptions waiting
## 1 3.600 79
## 2 1.800 54
## 3 3.333 74
## 4 2.283 62
## 5 4.533 85
## 6 2.883 55help("faithful")## starting httpd help server ... doneplot(faithful$waiting,faithful$eruptions)
fit = lm(eruptions ~ waiting, data=faithful)
summary(fit)##
## Call:
## lm(formula = eruptions ~ waiting, data = faithful)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.29917 -0.37689 0.03508 0.34909 1.19329
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.874016 0.160143 -11.70 <2e-16 ***
## waiting 0.075628 0.002219 34.09 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4965 on 270 degrees of freedom
## Multiple R-squared: 0.8115, Adjusted R-squared: 0.8108
## F-statistic: 1162 on 1 and 270 DF, p-value: < 2.2e-16plot(faithful$waiting,faithful$eruptions)
abline(coefficients(fit),col=2) A predição de novos valores pode ser feita com aplicação da função
A predição de novos valores pode ser feita com aplicação da função predict (prefira esse método) ou aplicação direta dos coeficientes. A predição ainda pode retornar o intervalo de confiança.
newdata = data.frame(waiting=c(80,110))
prediction = predict(fit, newdata)
prediction## 1 2
## 4.176220 6.445058# or
prediction = coefficients(fit)[1] + coefficients(fit)[2]*newdata
prediction## waiting
## 1 4.176220
## 2 6.445058# or
prediction = predict(fit, newdata, interval="predict")
prediction## fit lwr upr
## 1 4.176220 3.196089 5.156351
## 2 6.445058 5.450952 7.4391657.6 Regressão múltipla
O modelo acima pode ser aplicado diretamente a modelos de regressão linear múltipla adicionando à fórmula os atributos de cada variável de entrada.
fit = lm(y ~ atributo1 + atributo2 + ... , data=data)7.7 Exercícios
7.7.1 Exercício RESOLVIDO
Considere a base.
head(stackloss)## Air.Flow Water.Temp Acid.Conc. stack.loss
## 1 80 27 89 42
## 2 80 27 88 37
## 3 75 25 90 37
## 4 62 24 87 28
## 5 62 22 87 18
## 6 62 23 87 18help(stackloss)Qual a função linear que melhor aproxima stack.loss com base nos demais valores?
fit = lm(stack.loss ~ Air.Flow + Water.Temp + Acid.Conc., data=stackloss)
summary(fit)##
## Call:
## lm(formula = stack.loss ~ Air.Flow + Water.Temp + Acid.Conc.,
## data = stackloss)
##
## Residuals:
## Min 1Q Median 3Q Max
## -7.2377 -1.7117 -0.4551 2.3614 5.6978
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -39.9197 11.8960 -3.356 0.00375 **
## Air.Flow 0.7156 0.1349 5.307 5.8e-05 ***
## Water.Temp 1.2953 0.3680 3.520 0.00263 **
## Acid.Conc. -0.1521 0.1563 -0.973 0.34405
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.243 on 17 degrees of freedom
## Multiple R-squared: 0.9136, Adjusted R-squared: 0.8983
## F-statistic: 59.9 on 3 and 17 DF, p-value: 3.016e-09Portanto: \[ stack.loss = -39.92 + 0.7156 Air.Flow + 1.2953 Water.Temp + -0.1521 Acid.Conc. \] ### Exercício RESOLVIDO Faça uma predição do valor de stock.loss para os valores de Air.Flow=72, Water.Temp=20, Acid.Conc=85.
newdata = data.frame(Air.Flow=62, Water.Temp=23, Acid.Conc.=87)
prediction = predict(fit, newdata)
prediction## 1
## 21.006947.7.2 Exercício
O quanto esse valor difere do valor encontrado na base?
real = stackloss[stackloss$Air.Flow==62 & stackloss$Water.Temp==23 & stackloss$Acid.Conc ==87,]$stack.loss
real## [1] 18cat(( prediction - real )/ real * 100, '%')## 16.70522 %7.7.3 Exercício
Considere o exercício anterior. QUal variável contribuí mais positivamente para o incremento de stackloss?
Water.Temp
7.7.4 Exercício
Considere o exercício anterior. A regressão linear é uma boa aproximação dos dados (R-squared > 0.85)?
Sim. Adjusted R-squared: 0.8983
7.7.5 Exercício
Considere o exercício anterior. Elimine o atributo que não é significativo para a regressão e recalcule. O modelo obtido é melhor? (Verifique o R-squared). Dica: verifique o p-value dos coeficientes.
fit = lm(stack.loss ~ Air.Flow + Water.Temp , data=stackloss)
summary(fit)##
## Call:
## lm(formula = stack.loss ~ Air.Flow + Water.Temp, data = stackloss)
##
## Residuals:
## Min 1Q Median 3Q Max
## -7.5290 -1.7505 0.1894 2.1156 5.6588
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -50.3588 5.1383 -9.801 1.22e-08 ***
## Air.Flow 0.6712 0.1267 5.298 4.90e-05 ***
## Water.Temp 1.2954 0.3675 3.525 0.00242 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.239 on 18 degrees of freedom
## Multiple R-squared: 0.9088, Adjusted R-squared: 0.8986
## F-statistic: 89.64 on 2 and 18 DF, p-value: 4.382e-10Sim, R-squared maior e menor número de variáveis (hipóteses) no modelo.
7.7.6 Exercício
Considere a base iris (builtin do R). Calcule a regressão linear para obter o comprimento de petalas (sepalas) a partir da largura. Qual apresenta melhor coeficiente de determinação? Pétalas ou Sépalas?
# Sua resposta7.7.7 Exercício
Considere a base.
df = read.csv('https://meusite.mackenzie.br/rogerio/TIC/FuelConsumptionCo2.csv',header=T)
head(df)## MODELYEAR MAKE MODEL VEHICLECLASS ENGINESIZE CYLINDERS TRANSMISSION
## 1 2014 ACURA ILX COMPACT 2.0 4 AS5
## 2 2014 ACURA ILX COMPACT 2.4 4 M6
## 3 2014 ACURA ILX HYBRID COMPACT 1.5 4 AV7
## 4 2014 ACURA MDX 4WD SUV - SMALL 3.5 6 AS6
## 5 2014 ACURA RDX AWD SUV - SMALL 3.5 6 AS6
## 6 2014 ACURA RLX MID-SIZE 3.5 6 AS6
## FUELTYPE FUELCONSUMPTION_CITY FUELCONSUMPTION_HWY FUELCONSUMPTION_COMB
## 1 Z 9.9 6.7 8.5
## 2 Z 11.2 7.7 9.6
## 3 Z 6.0 5.8 5.9
## 4 Z 12.7 9.1 11.1
## 5 Z 12.1 8.7 10.6
## 6 Z 11.9 7.7 10.0
## FUELCONSUMPTION_COMB_MPG CO2EMISSIONS
## 1 33 196
## 2 29 221
## 3 48 136
## 4 25 255
## 5 27 244
## 6 28 230Construa um modelo de regressão para:
plot(df$FUELCONSUMPTION_COMB, df$CO2EMISSIONS)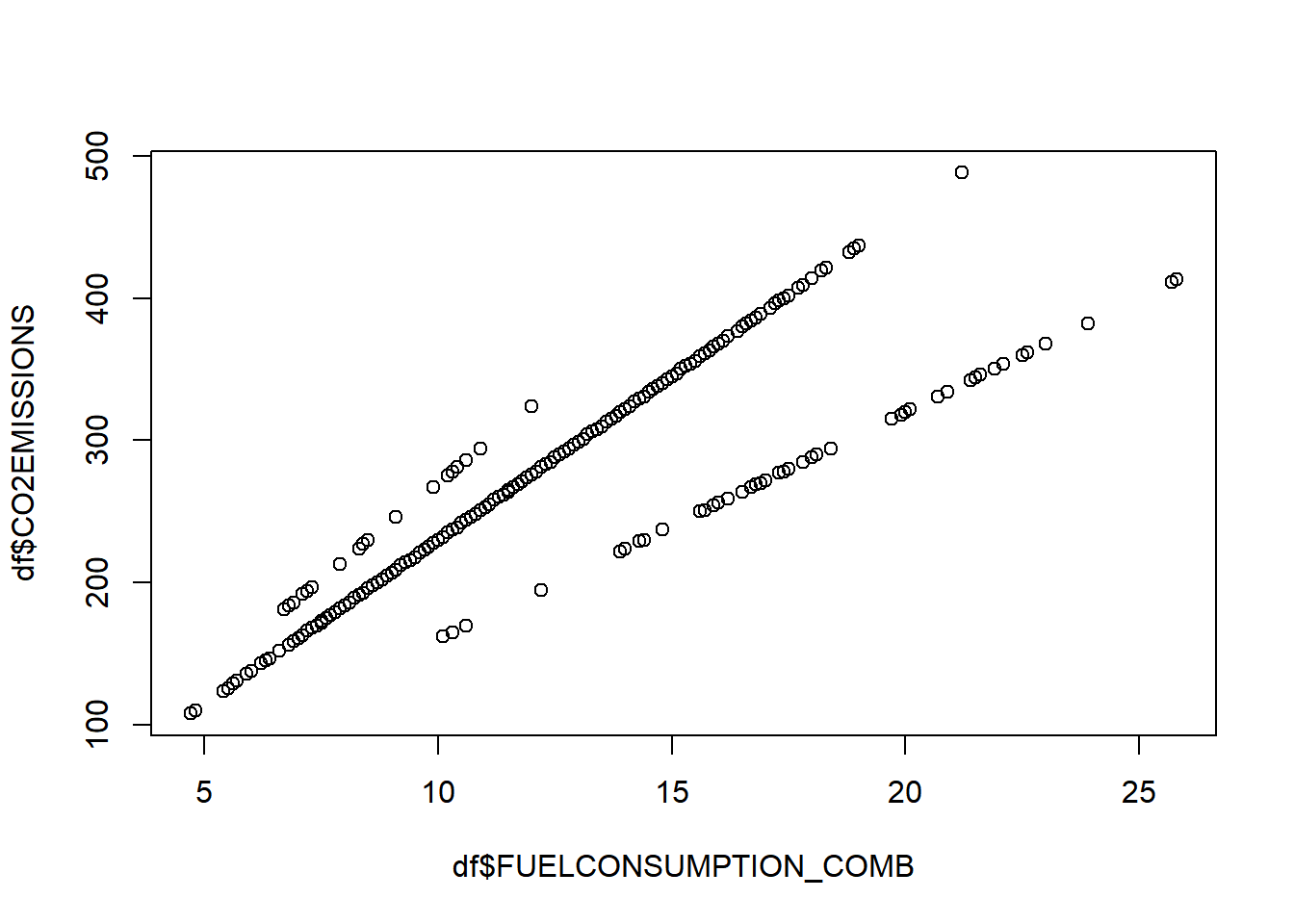
# Sua resposta7.7.8 Exercício
Estime as emissões de CO2EMISSIONS a partir de valores de FUELCONSUMPTION_COMB para os valores 4 e 28
# sua resposta7.7.9 Exercício
Acrescente ao seu modelo a variável de entrada ENGINESIZE. Qual a função e o R-Square obtidos? É um modelo melhor que o somente baseado em FUELCONSUMPTION_COMB como variável independente?
# sua resposta7.7.10 Exercício
Faça a predição de CO2EMISSIONS com base no modelo anterior, para FUELCONSUMPTION_COMB = 10 e ENGINESIZE=2.
# sua resposta7.7.11 Exercício
Acrescente ao modelo anterior o atributo VEHICLECLASS. Note VEHICLECLASS é um atributo categórico. Você precisará fazer o Hot Encode do atributo antes
Dica:
library(dummies)## dummies-1.5.6 provided by Decision Patternsdf = dummy.data.frame('VEHICLECLASS',data=df,sep='.',drop=FALSE)
colnames(df)## [1] "MODELYEAR"
## [2] "MAKE"
## [3] "MODEL"
## [4] "VEHICLECLASS.COMPACT"
## [5] "VEHICLECLASS.FULL-SIZE"
## [6] "VEHICLECLASS.MID-SIZE"
## [7] "VEHICLECLASS.MINICOMPACT"
## [8] "VEHICLECLASS.MINIVAN"
## [9] "VEHICLECLASS.PICKUP TRUCK - SMALL"
## [10] "VEHICLECLASS.PICKUP TRUCK - STANDARD"
## [11] "VEHICLECLASS.SPECIAL PURPOSE VEHICLE"
## [12] "VEHICLECLASS.STATION WAGON - MID-SIZE"
## [13] "VEHICLECLASS.STATION WAGON - SMALL"
## [14] "VEHICLECLASS.SUBCOMPACT"
## [15] "VEHICLECLASS.SUV - SMALL"
## [16] "VEHICLECLASS.SUV - STANDARD"
## [17] "VEHICLECLASS.TWO-SEATER"
## [18] "VEHICLECLASS.VAN - CARGO"
## [19] "VEHICLECLASS.VAN - PASSENGER"
## [20] "ENGINESIZE"
## [21] "CYLINDERS"
## [22] "TRANSMISSION"
## [23] "FUELTYPE"
## [24] "FUELCONSUMPTION_CITY"
## [25] "FUELCONSUMPTION_HWY"
## [26] "FUELCONSUMPTION_COMB"
## [27] "FUELCONSUMPTION_COMB_MPG"
## [28] "CO2EMISSIONS"Além disso a função lm não aceita atributos com '_' ou brancos!
# sua resposta