4. Evolução¶
Com o instrumental básico que vimos até aqui você pode começar a explorar diferentes dados.
Neste capítulo vamos estar interessados em observar a evolução de um conjunto de dados, o comportamento de uma ou mais variáveis dependentes, com relação ao crescimento de uma outra variável independente. Quando a evolução é observada ao longo do tempo, chamaremos esse conjunto de série temporal.
Vários conjuntos de dados de interesse apresentam essas características, como funções em geral e séries de dados históricas. Séries históricas de valores do PIB, número de internações diárias em um hospital, hits diários em um site de e-commerce ou a evolução das emissões de CO2 ao longo do tempo, para citar alguns exemplos.
Gráficos de linha, como os que empregamos até aqui, são comumente usados para observar a evolução dos dados. Mas antes de prosseguirmos vamos entender uma diferença entre gráficos de funções que fizemos até aqui e gráficos que exploram dados em geral.
4.1. Funções, Equações e Dados¶
Nos exemplos anteriores empregamos funções para aprender um conjunto de comandos essencias para a produção de gráficos. Funções são um mapeamento em que para a cada dado de entrada (variáveis independentes) corresponde uma única variável de saída (variável dependente). Muitas funções são modeladas por Equações, como os modelos físicos de força (\(F = m \alpha\)) ou da cinemática, há diversos modelos em diferentes áreas como engenharia, economia, biologia e mesmo nas ciências sociais, e modelos mais complexos podem evolver todo um sistema de equações.
4.2. Modelo do Lançamento de um Projétil¶
Embora essas equações desempenhem um papel fundamental em muitos problemas, a análise de dados em geral emprega a coleta de dados reais que diferem parcialmente dos modelos pela simplificação da realidade que eles adotam (desprezar o atrito por exemplo). É comum os dados apresentarem mais de um valor para uma mesma entrada de dados, como no caso de coleta de vários experimentos ou indivíduos, não sendo assim, neste caso, uma função no sentido matemático do termo (funções, por definição, apresentam sempre um único valor para a mesma entrada). Além disso, uma série de dados pode nem mesmo corresponder a qualquer modelo de equações conhecido, bastando lembrar de dados da bolsa de valores, do PIB ou ainda da progressão de casos de epidemia em uma população.
O exemplo a seguir ilustra a diferença entre empregarmos equações para produzir visualizações, como fizemos até aqui, e o emprego de dados obtidos por coleta.
Neste exemplo empregamos o modelo físico de lançamento de um projétil. A posição do projétil ao longo da sua trajetória pode ser dado em função da sua velocidade inicial e o ângulo de lançamento do projétil:
o primeiro gráfico abaixo corresponde a essa trajetória teórica.
Se você já acompanhou algum experimento em um laboratório de física ou química, pode imaginar que uma coleta de dados de vários lançamentos do projeto deve produzir resultados ligeiramente diferentes, seja por elementos não considerados no modelo como atrito, velocidade do ar etc. seja por imprecisões na tomada das medidas. Aqui, simulamos essas coletas adicionando ruído ao modelo teórico reproduzindo assim os dados reais do experimento. Note que para a exibição desses dados (segundo gráfico) empregamos a função plt.scatter e não o plot de linhas. O scatter plot é um gráfico de pontos ou de dispersão dos dados. Ele não liga os pontos de dados por linhas e é útil para exibir como estão dispersos os valores dos dados de duas variáveis. Falaremos mais sobre ele adiante e no capítulo Relações. Por hora ele é útil para exibir vários dados nos quais buscamos observar ou construir uma linha de tendência.
\(\bigstar \text{ }\)
scatterplot é um gráfico de pontos ou de dispersão dos dados. Ele não liga os pontos de dados por linhas e é útil para exibir como estão dispersos os valores dos dados com relação a duas variáveis.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
%matplotlib inline
O código abaixo produz os dados da trajetória do projétil e você pode pular se não estiver interessado nos detalhes de como produzimos esses dados.
# Cálculo da trajetória do projétil
def calc(iAngulo=45, iV0=100):
angRAd = np.deg2rad(iAngulo)
g = 9.8
alcanceMax = round(((iV0**2) * np.sin(2*angRAd)) / g, 1)
alturaMax = round((iV0**2) * (np.sin(angRAd))**2 / (2*g), 1)
tempoTotal = round((((2*iV0) * np.sin(angRAd)) / g), 1)
t = np.arange(0, tempoTotal, 0.25)
x = abs(iV0) * np.cos(angRAd) * t
y = (abs(iV0) * np.sin(angRAd) * t) - ((g*(t**2))/2)
vx = abs(iV0) * np.cos(angRAd) * ( t*0 + 1 )
vy = abs( abs(iV0) * np.sin(angRAd) * ( t*0 + 1 ) - g*t )
return t,x,y,vx,vy
# Cálculo das trajetórias para lançamentos em ângulos de 45, 30 e 60 graus
t,x,y,vx,vy = calc(45)
A = np.ones(len(t))*45
M = np.ones(len(t))
df_teorico = pd.DataFrame(zip(M,A,t,x,y), columns=['medida','angulo','t','x','y'])
t,x,y,vx,vy = calc(30)
A = np.ones(len(x))*30
M = np.ones(len(t))
df_teorico = pd.concat([df_teorico, pd.DataFrame(zip(M,A,t,x,y), columns=['medida','angulo','t','x','y'])])
t,x,y,vx,vy = calc(60)
A = np.ones(len(x))*60
M = np.ones(len(t))
df_teorico = pd.concat([df_teorico, pd.DataFrame(zip(M,A,t,x,y), columns=['medida','angulo','t','x','y'])])
# Simulando medidas de 20 lançamentos adicionando ruído ao modelo teórico
df_real = pd.DataFrame()
for i in range(20):
df_med = df_teorico.copy()
df_med.medida = i
df_med.x += df_med.x * np.random.normal(0,1,len(df_med))/65
df_med.y += df_med.y * np.random.normal(0,1,len(df_med))/65
df_real = pd.concat([df_real, df_med])
Dados do lançamento teórico e do lançamentos reais simulados:
df_teorico.head()
| medida | angulo | t | x | y | |
|---|---|---|---|---|---|
| 0 | 1.0 | 45.0 | 0.00 | 0.000000 | 0.000000 |
| 1 | 1.0 | 45.0 | 0.25 | 17.677670 | 17.371420 |
| 2 | 1.0 | 45.0 | 0.50 | 35.355339 | 34.130339 |
| 3 | 1.0 | 45.0 | 0.75 | 53.033009 | 50.276759 |
| 4 | 1.0 | 45.0 | 1.00 | 70.710678 | 65.810678 |
df_real.head()
| medida | angulo | t | x | y | |
|---|---|---|---|---|---|
| 0 | 0 | 45.0 | 0.00 | 0.000000 | 0.000000 |
| 1 | 0 | 45.0 | 0.25 | 17.535999 | 17.292727 |
| 2 | 0 | 45.0 | 0.50 | 35.003802 | 34.090802 |
| 3 | 0 | 45.0 | 0.75 | 53.055385 | 50.719787 |
| 4 | 0 | 45.0 | 1.00 | 70.604766 | 66.087010 |
Gráficos dos dados de lançamento.
fig, ax = plt.subplots(1,2,figsize=(12,6),sharey=True)
# Gráficos
for ang in [45,30,60]:
ax[0].plot(df_teorico[df_teorico.angulo == ang].x, df_teorico[df_teorico.angulo == ang].y, '-', label='$a_0 = $' + str(ang))
for ang in [45,30,60]:
ax[1].scatter(df_real[df_real.angulo == ang].x, df_real[df_real.angulo == ang].y, s=2.5, alpha=0.6)
ax[1].plot(df_teorico[df_teorico.angulo == ang].x, df_teorico[df_teorico.angulo == ang].y, '--', label='$\\alpha = $' + str(ang) + '$^o$')
# Anotações
for i in range(2):
ax[i].text(320, 50, '$ x = V_{0} cos(\\alpha) t $', fontsize=11)
ax[i].text(320, 30, '$ y = V_{0} sin(\\alpha) t - g t^2 / 2 $', fontsize=11)
ax[i].set_xlabel("Distância (m)")
ax[0].set_title("Trajetória Teórica do Lançamento", fontsize=14, weight='bold')
ax[1].set_title("Trajetória de várias Medidas de Lançamento", fontsize=14, weight='bold')
ax[0].set_ylabel("Altura (m)")
plt.legend(fontsize=12)
plt.tight_layout()
plt.show()
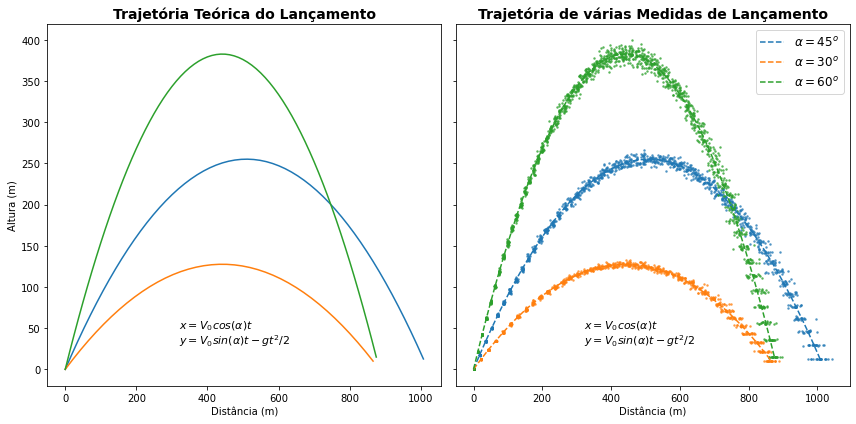
Você pode notar que o último gráfico não corresponde exatamente a uma função. Em especial, no caso das várias medidas, encontramos diferentes valores de \(x\) e \(y\) para os mesmos instantes de tempo. Não encontramos também a monotonicidade (dados crescentes ou descrecentes em um intervalo) ou a continuidade que normalmente exibem as funções, já que os pontos consideram um conjunto discreto e não contínuo de dados.
(*) A rigor aqui \(x\) e \(y\) são função do tempo \(t\), isto é \(x(t), y(t)\). Entretanto, exibimos um gráfico de \(x \times y\). Isso pode ser feito por haver uma correspondência direta do valor de \(x\) e de \(t\), enquanto também parece ser muito mais interessante exibir a trajetória dos lançamentos. A tabela da função pode ser vista df_teorico.head().
4.3. Modelo de uma Turbina Eólica¶
Você talvez considere o modelo anterior muito elementar e imagine que casos como esse não encontrem paralelo em casos mais práticos. Vamos então empregar um exemplo real.
A seguir você encontra os dados de um modelo teórico da energia produzida por uma turbina heólica em função da velocidade do vento e os dados reais de turbinas obtidos a partir de medições. Aqui o modelo teórico é muito mais complexo do que modelo físico anterior com várias equações que envolvem parâmetros da turbina, condições de funcionamento, diâmetro da hélice, direção do vento etc. Já os dados reais são medidas diretas de turbinas em operação.
O modelo teórico é útil pois permite comparar o modelo com os dados reais como abaixo.
data_T_AA = pd.read_csv('https://raw.githubusercontent.com/Rogerio-mack/Visualizacao-de-Dados-em-Python/main/data/T1_reshape.csv')
data_T_AA_mean = pd.read_csv('https://raw.githubusercontent.com/Rogerio-mack/Visualizacao-de-Dados-em-Python/main/data/T1_reshape_mean.csv')
data_T_AA.head()
| WindSpeed(m/s) | ActivePower(kW) | Theoretical_Power_Curve (KWh) | Loss_Value(kW) | Loss(%) | count | direction | |
|---|---|---|---|---|---|---|---|
| 0 | 3.5 | 43.46 | 70.58 | 27.12 | 38.02 | 29 | N |
| 1 | 4.0 | 88.01 | 127.57 | 39.56 | 31.60 | 101 | N |
| 2 | 4.5 | 160.51 | 217.01 | 56.50 | 26.42 | 102 | N |
| 3 | 5.0 | 274.71 | 335.67 | 60.96 | 18.44 | 99 | N |
| 4 | 5.5 | 388.60 | 465.84 | 77.24 | 16.79 | 119 | N |
data_T_AA_mean.head()
| WindSpeed(m/s) | ActivePower(kW) | Theoretical_Power_Curve (KWh) | Loss_Value(kW) | Loss(%) | count | |
|---|---|---|---|---|---|---|
| 0 | 3.5 | 52.191667 | 68.939167 | 16.745833 | 23.584167 | 56.250000 |
| 1 | 4.0 | 97.756667 | 127.686667 | 29.929167 | 23.646667 | 144.666667 |
| 2 | 4.5 | 183.601667 | 221.930000 | 38.327500 | 17.488333 | 149.500000 |
| 3 | 5.0 | 286.590833 | 336.426667 | 49.835000 | 14.937500 | 143.750000 |
| 4 | 5.5 | 400.392500 | 470.090833 | 69.699167 | 14.838333 | 167.666667 |
fig, ax = plt.subplots(1,2,figsize=(12,6),sharey=True)
fig.suptitle('Modelo e dados reais de uma Turbina Eólica', fontsize=14, weight='bold', y=1.05)
# Gráficos
ax[0].plot(data_T_AA_mean["WindSpeed(m/s)"],data_T_AA_mean["Theoretical_Power_Curve (KWh)"])
ax[1].plot(data_T_AA_mean["WindSpeed(m/s)"],data_T_AA_mean["Theoretical_Power_Curve (KWh)"], '--k', label='Theorical')
ax[1].scatter(data_T_AA["WindSpeed(m/s)"],data_T_AA["ActivePower(kW)"], label='Real', marker='o', color='orange', alpha=0.5)
ax[0].set_title("Curva de Energia Teória (KWh)", fontsize=14, weight='bold')
ax[1].set_title("Energia Real - Várias Turbinas (KWh)", fontsize=14, weight='bold')
ax[0].set_ylabel("Power (KWh)")
# Anotações
ax[0].set_xlabel("WindSpeed(m/s)")
ax[1].set_xlabel("WindSpeed(m/s)")
plt.legend(loc='lower right',fontsize=12)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.tight_layout()
plt.show()
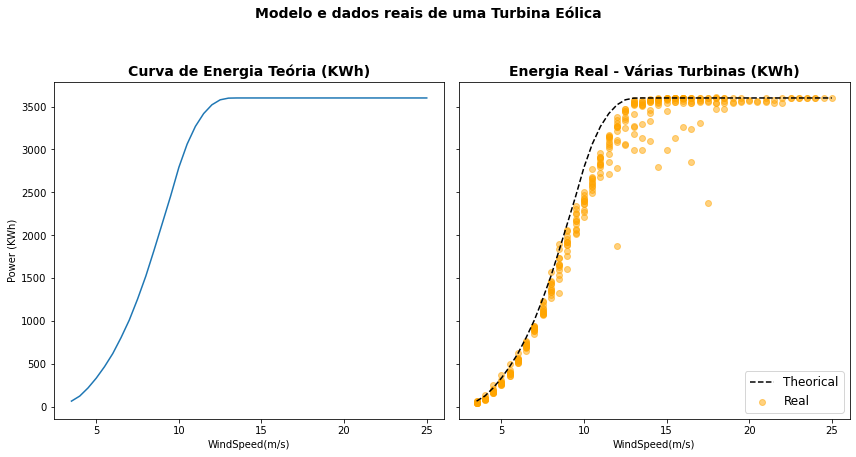
O modelo permite observar como comportam-se as turbinas reais com relação ao modelo teórico no que se refere a energia produzida, e você pode reparar a dipersão dos valores das diferentes turbinas ou ainda os resultados bastante abaixo do modelo teórico do fabricante para a faixa de velocidade do vento entre 9-12 m/s.
4.4. Covid, Bolsa e Google Trends¶
Mas ainda há uma classe de dados em que parece ser ainda mais importante a visualização dos dados. No conjunto de dados anterior existe um modelo teórico e um conjunto de dados reais, mas muitos conjuntos de dados não tem nenhum modelo teórico conhecido o que torna a análise e a busca por padrões nesses dados talvez muito mais importante.
Os três exemplos que seguem mostram respectivamente, para um mesmo perído de 2020, (a) a evolução de novos casos de Covid no Brasil, (b) dados do Ibovespa e (c) da pesquisa de termos no Google (Google Trends). Para nenhum desses dados existe um modelo teórico conhecido, mas podemos, a partir da visualização desses dados observar sua evolução e verificar hipóteses e possíveis causas para os comportamentos observados.
4.4.1. (a) Covid 2020¶
from datetime import datetime
corona_Brasil = pd.read_csv('https://raw.githubusercontent.com/Rogerio-mack/Visualizacao-de-Dados-em-Python/main/data/corona_Brasil.csv')
corona_Brasil.data = pd.to_datetime(corona_Brasil.data, format='%Y-%m-%d',errors='coerce')
corona_Brasil.head()
| regiao | estado | municipio | coduf | codmun | codRegiaoSaude | nomeRegiaoSaude | data | semanaEpi | populacaoTCU2019 | casosAcumulado | casosNovos | obitosAcumulado | obitosNovos | Recuperadosnovos | emAcompanhamentoNovos | interior/metropolitana | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Brasil | NaN | NaN | 76 | NaN | NaN | NaN | 2020-02-25 | 9.0 | 210147125.0 | 0.0 | 0.0 | 0.0 | 0.0 | NaN | NaN | NaN |
| 1 | Brasil | NaN | NaN | 76 | NaN | NaN | NaN | 2020-02-26 | 9.0 | 210147125.0 | 1.0 | 1.0 | 0.0 | 0.0 | NaN | NaN | NaN |
| 2 | Brasil | NaN | NaN | 76 | NaN | NaN | NaN | 2020-02-27 | 9.0 | 210147125.0 | 1.0 | 0.0 | 0.0 | 0.0 | NaN | NaN | NaN |
| 3 | Brasil | NaN | NaN | 76 | NaN | NaN | NaN | 2020-02-28 | 9.0 | 210147125.0 | 1.0 | 0.0 | 0.0 | 0.0 | NaN | NaN | NaN |
| 4 | Brasil | NaN | NaN | 76 | NaN | NaN | NaN | 2020-02-29 | 9.0 | 210147125.0 | 2.0 | 1.0 | 0.0 | 0.0 | NaN | NaN | NaN |
fig, ax = plt.subplots(figsize=(14,6))
ax.plot(corona_Brasil.data, corona_Brasil.casosNovos, label='Novos Casos')
ax.set_title('Novos Casos de Covid (Brasil)', fontsize=14, weight='bold')
ax.set_xlabel("date")
ax.set_ylabel("Novos Casos")
ax.legend()
plt.show()
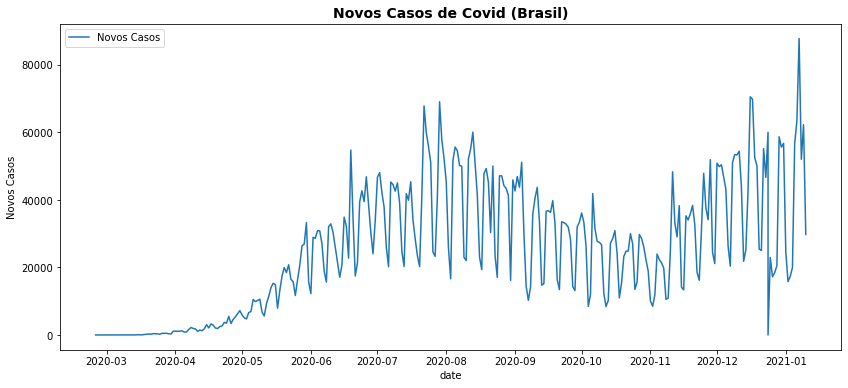
4.4.2. (b) Ibovepa 2020¶
bovespa = pd.read_csv('https://raw.githubusercontent.com/Rogerio-mack/Visualizacao-de-Dados-em-Python/main/data/mystocksn.csv')
bovespa.data = pd.to_datetime(bovespa.data, format='%Y-%m-%d',errors='coerce') # somente para ajustar formato da datas
bovespa.head()
| data | IBOV | VALE3 | PETR4 | DOLAR | |
|---|---|---|---|---|---|
| 0 | 2020-02-27 | 102984.0 | 9.92 | 12.08 | 4.4491 |
| 1 | 2020-02-28 | 104172.0 | 9.82 | 12.10 | 4.4848 |
| 2 | 2020-03-02 | 106625.0 | 10.27 | 12.49 | 4.4413 |
| 3 | 2020-03-03 | 105537.0 | 10.22 | 12.16 | 4.4724 |
| 4 | 2020-03-04 | 107224.0 | 10.56 | 12.33 | 4.5132 |
fig, ax = plt.subplots(figsize=(14,6))
ax.plot(bovespa.data, bovespa.VALE3, label='VALE3')
ax.plot(bovespa.data, bovespa.PETR4, label='PETR4')
ax.plot(bovespa.data, bovespa.DOLAR, label='DOLAR')
ax.set_title('Bolsa Ações', fontsize=14, weight='bold')
ax.set_xlabel("date")
ax.set_ylabel("Valor (R$)")
ax.legend(fontsize=12)
import matplotlib.ticker as ticker
ax.xaxis.set_major_locator(ticker.MaxNLocator(8))
plt.show()
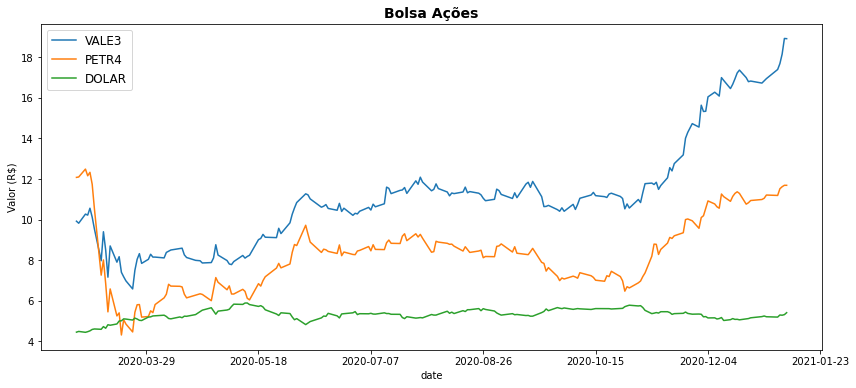
4.4.3. (c) Google Trends¶
# Este código apenas instala o pacotes para buscar dados do Google Trends e você pode querer empregá-lo para fazer suas próprias pesquisas.
!pip install pytrends
from pytrends.request import TrendReq
pytrend = TrendReq()
Requirement already satisfied: pytrends in c:\users\user\anaconda3\lib\site-packages (4.7.3)
Requirement already satisfied: pandas>=0.25 in c:\users\user\anaconda3\lib\site-packages (from pytrends) (1.1.3)
Requirement already satisfied: requests in c:\users\user\anaconda3\lib\site-packages (from pytrends) (2.24.0)
Requirement already satisfied: lxml in c:\users\user\anaconda3\lib\site-packages (from pytrends) (4.6.1)
Requirement already satisfied: pytz>=2017.2 in c:\users\user\anaconda3\lib\site-packages (from pandas>=0.25->pytrends) (2020.1)
Requirement already satisfied: python-dateutil>=2.7.3 in c:\users\user\anaconda3\lib\site-packages (from pandas>=0.25->pytrends) (2.8.1)
Requirement already satisfied: numpy>=1.15.4 in c:\users\user\anaconda3\lib\site-packages (from pandas>=0.25->pytrends) (1.19.2)
Requirement already satisfied: certifi>=2017.4.17 in c:\users\user\anaconda3\lib\site-packages (from requests->pytrends) (2020.12.5)
Requirement already satisfied: chardet<4,>=3.0.2 in c:\users\user\anaconda3\lib\site-packages (from requests->pytrends) (3.0.4)
Requirement already satisfied: urllib3!=1.25.0,!=1.25.1,<1.26,>=1.21.1 in c:\users\user\anaconda3\lib\site-packages (from requests->pytrends) (1.25.11)
Requirement already satisfied: idna<3,>=2.5 in c:\users\user\anaconda3\lib\site-packages (from requests->pytrends) (2.10)
Requirement already satisfied: six>=1.5 in c:\users\user\anaconda3\lib\site-packages (from python-dateutil>=2.7.3->pandas>=0.25->pytrends) (1.15.0)
pytrend.build_payload(kw_list=['Covid','Hotel','NetFlix','Notebook'], cat=0, timeframe='2020-02-25 2021-01-10', geo='BR')
trends = pytrend.interest_over_time()
trends.head()
| Covid | Hotel | NetFlix | Notebook | isPartial | |
|---|---|---|---|---|---|
| date | |||||
| 2020-03-01 | 2 | 42 | 36 | 16 | False |
| 2020-03-08 | 9 | 38 | 33 | 16 | False |
| 2020-03-15 | 61 | 21 | 64 | 18 | False |
| 2020-03-22 | 76 | 14 | 81 | 23 | False |
| 2020-03-29 | 66 | 14 | 70 | 24 | False |
fig, ax = plt.subplots(figsize=(14,6))
# Gráficos
ax.plot(trends.index, trends.Covid, label='Covid')
ax.plot(trends.index, trends.Hotel, label='Hotel')
ax.plot(trends.index, trends.NetFlix, label='NetFlix')
ax.plot(trends.index, trends.Notebook, label='Notebook')
# Anotações
from datetime import datetime
ax.set_title('Google Trends', fontsize=14, weight='bold')
ax.set_xlabel("date")
ax.set_ylabel("% hits")
ax.legend(fontsize=12)
plt.show()
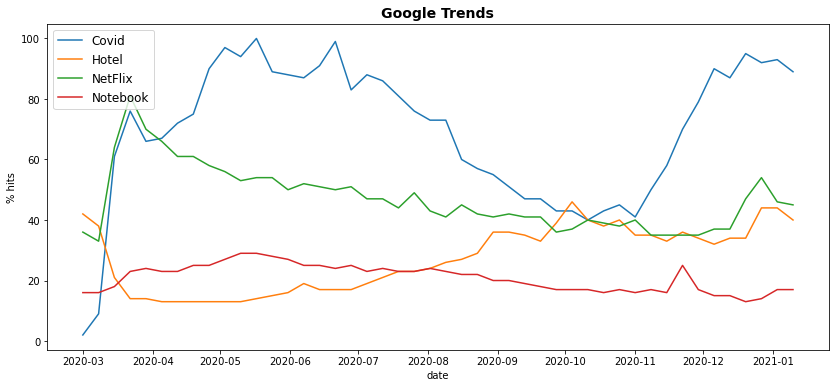
E podemos então empregar todos esses dados juntos para entendermos melhor a evolução desses dados.
fig, ax = plt.subplots(3,1,figsize=(14,15), sharex=True)
fig.suptitle('Evolução de Dados sem Modelos Conhecidos', fontsize=14, weight='bold')
ax[0].plot(corona_Brasil.data, corona_Brasil.casosNovos, label='Casos Novos')
# Linhas verticais
ax[0].vlines(datetime(2020, 3, 22),0,corona_Brasil.casosNovos.max(),linewidth=1,linestyle='--',colors='grey')
ax[0].vlines(datetime(2020, 11, 1),0,corona_Brasil.casosNovos.max(),linewidth=1,linestyle='--',colors='grey')
ax[0].set_title('Novos Casos de Covid (Brasil)', fontsize=14, weight='bold')
ax[0].set_xlabel("date")
ax[0].set_ylabel("Novos Casos")
import numpy as np
x = np.arange(0,len(corona_Brasil),1)
z = np.polyfit(x, corona_Brasil.casosNovos, 1)
p = np.poly1d(z)
ax[0].plot(corona_Brasil.data,p(x),color='darkorange', linestyle='dashed')
# Annotate
ax[0].annotate('Segunda onda da Covid-19 no Brasil',
xy=(datetime(2020, 11, 1), 50000), # ponto do gráfico
xytext=(datetime(2020, 8, 15), 70000), # posição do texto
arrowprops=dict(arrowstyle="->"),
fontsize=12,
color='grey')
ax[0].legend()
ax[1].plot(bovespa.data, bovespa.VALE3, label='VALE3')
ax[1].plot(bovespa.data, bovespa.PETR4, label='PETR4')
ax[1].plot(bovespa.data, bovespa.DOLAR, label='DOLAR')
# Linhas verticais
ax[1].vlines(datetime(2020, 3, 22),0,bovespa.VALE3.max(),linewidth=1,linestyle='--',colors='grey')
ax[1].vlines(datetime(2020, 11, 1),0,bovespa.VALE3.max(),linewidth=1,linestyle='--',colors='grey')
ax[1].set_title('Bolsa Ações', fontsize=14, weight='bold')
ax[1].set_xlabel("date")
ax[1].set_ylabel("Valor (R$)")
# Annotate
ax[1].annotate('Impacto da Primeira onda \n Covid-19 no Brasil',
xy=(datetime(2020, 3, 22), 10), # ponto do gráfico
xytext=(datetime(2020, 4, 1),15), # posição do texto
arrowprops=dict(arrowstyle="->"),
fontsize=12,
color='grey')
import matplotlib.ticker as ticker
ax[1].xaxis.set_major_locator(ticker.MaxNLocator(8))
ax[1].legend(fontsize=12)
ax[2].plot(trends.index, trends.Covid, label='Covid')
ax[2].plot(trends.index, trends.Hotel, label='Hotel')
ax[2].plot(trends.index, trends.NetFlix, label='NetFlix')
ax[2].plot(trends.index, trends.Notebook, label='Notebook')
# Linhas verticais
ax[2].vlines(datetime(2020, 3, 22),0,100,linewidth=1,linestyle='--',colors='grey')
ax[2].vlines(datetime(2020, 11, 1),0,100,linewidth=1,linestyle='--',colors='grey')
ax[2].set_title('Google Trends', fontsize=14, weight='bold')
ax[2].set_xlabel("date")
ax[2].set_ylabel("% hits")
ax[2].legend()
plt.legend(loc='upper left',fontsize=12)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()
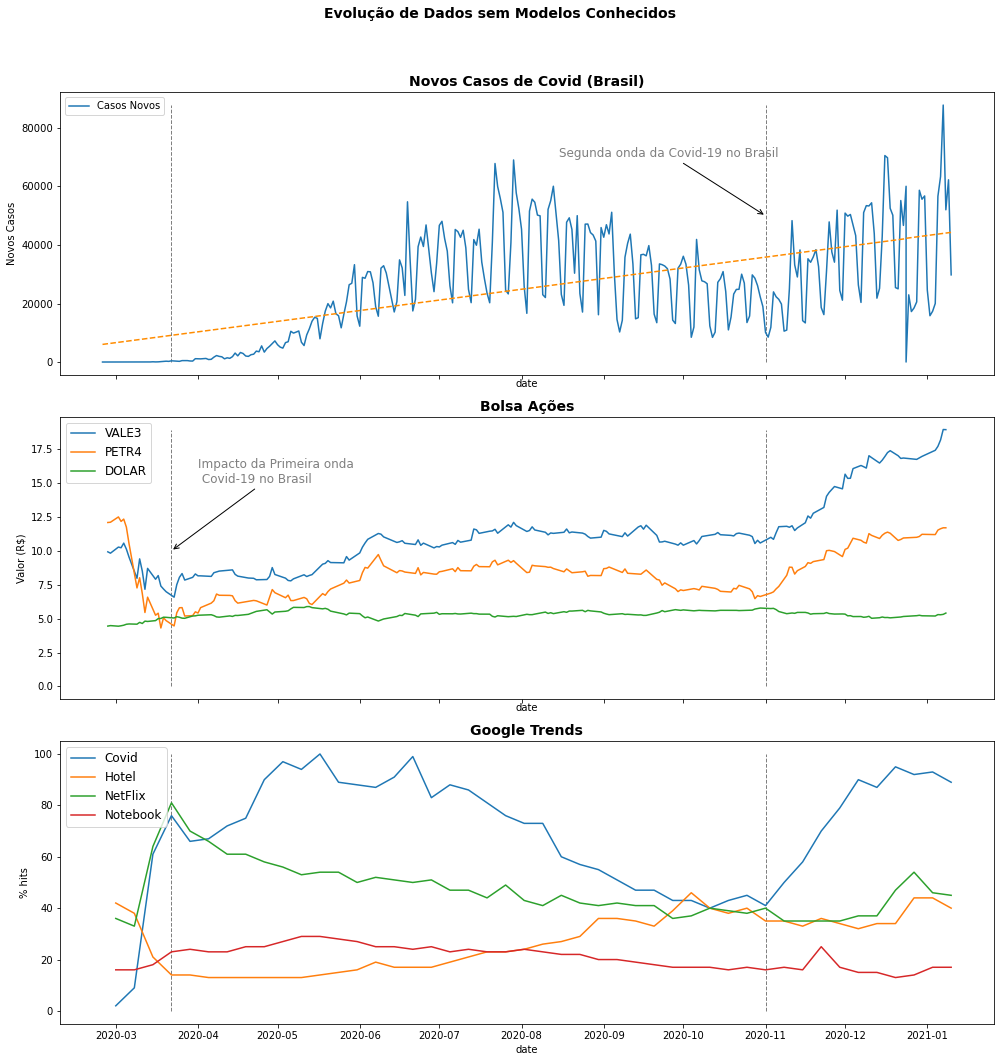
A visualização nos ajuda, por exemplo, observarmos os impactos da pandemia sobre os ativos da bolsa (queda dos preços, aumento do dólar) e ou as buscas na internet (aumento de busca por serviços de streamming, queda de busca por hotéis).
É claro que observar a evolução dos dados ou suas tendências não significa entender essa evolução e essas relações. Mas a visualização, na ausência de modelos teóricos, exibe esses comportamentos para que possam ser melhor analisados e entendidos. Note ainda que, além de explorarmos a evolução dos dados, estamos aqui observando relações entre os gráficos e uma visualização pode explorar vários aspectos dos dados. Mas aqui estamos interessados na evolução dos dados e no capítulo de Relações você verá mais sobre isso.
Obviamente não vamos fazer uma análise completa e conclusiva desses dados aqui, mas podemos ter uma ideia das relações entre buscas de termos no Google, a evolução de casos de Covid e seus impactos na Bolsa, e pode observar aqui o potencial de empregarmos a visualização de dados para entender a evolução desses dados e vamos ver mais algumas técnicas úteis para análise a partir de gráficos de linha como adicionar linhas de tendências aos dados e lidar com diferentes escalas de dados.
4.5. Adicionando linhas de Tendência¶
Adicionar uma linha de tendência pressupõe fazermos algum tipo de modelo de regressão sobre os dados. Fizemos isso acima no gráfico de evolução dos casos de Covid. Em geral isso envolve escolhermos um tipo de função (linear, polinomial, exponencial etc.) e, em seguida determinarmos os parâmetros dessa função a partir, por exemplo, de um método de otimização como o de mínimos quadrados.
Essa pode ser uma tarefa bastante complexa e o Matplotlib não tem um função direta para produzir essas linhas de tendência. Mas podemos fazer uso de outros pacotes Python para isso e, no final, a solução é bastante simples e flexível pois permite empregar muitos outros métodos de regressão, incluinco modelos sofisticados de aprendizado de máquina.
Vamos começar com um conjunto de dados simples que já conhecemos, o quarteto de dados de Anscombe.
import seaborn as sns
# Load the example dataset for Anscombe's quartet
df = sns.load_dataset("anscombe")
df.head()
| dataset | x | y | |
|---|---|---|---|
| 0 | I | 10.0 | 8.04 |
| 1 | I | 8.0 | 6.95 |
| 2 | I | 13.0 | 7.58 |
| 3 | I | 9.0 | 8.81 |
| 4 | I | 11.0 | 8.33 |
4.5.1. Aproximando por um polinômio np.polyfit()¶
A função np.polyfit() do pacote NumPy pode ser empregada para se obter os coeficientes de um polinômino de grau qualquer que melhor aproxima um conjunto de pontos. Se empregada com o grau 1 a aproximação irá corresponder ao modelo de regressão linear encontrando a melhor representação dos dados por uma reta.
O uso é bastante direto:
z = np.polyfit(ds.x, ds.y, 2)
p = np.poly1d(z)
A função np.polyfit(x,y,<grau>) é um otimizador e faz o cálculo dos coeficientes do polinômio \(p( )\) que melhor aproxima os dados \(y = p(x)\) com o grau indicado. A função p = np.poly1d(z) retorna o polinômio em forma de uma função que pode ser então aplicada a qualquer conjunto de dados. Um comando x = np.arange() pode ser empregado para gerar um intervalo de valores em que desejamos aplicar o polinômio p, para exibir uma linha contínua plt.plot(x,p(x)).
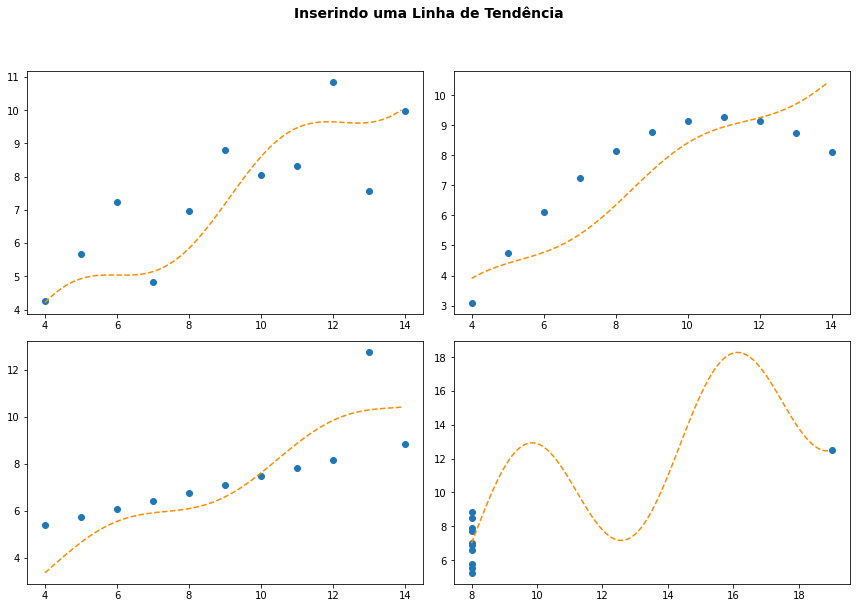
fig, ax = plt.subplots(2,2,figsize=(12,8))
fig.suptitle('Inserindo uma Linha de Tendência', fontsize=14, weight='bold', y=1.05)
i = 0
for ds_type in df.dataset.unique():
ds = df[df.dataset == ds_type]
z = np.polyfit(ds.x, ds.y, 1)
p = np.poly1d(z)
ax[i//2,i%2].scatter(ds.x,ds.y)
x = np.arange(ds.x.min(), ds.x.max(), 0.1)
ax[i//2,i%2].plot(x,p(x),color='darkorange', linestyle='dashed')
i += 1
plt.tight_layout()
plt.show()
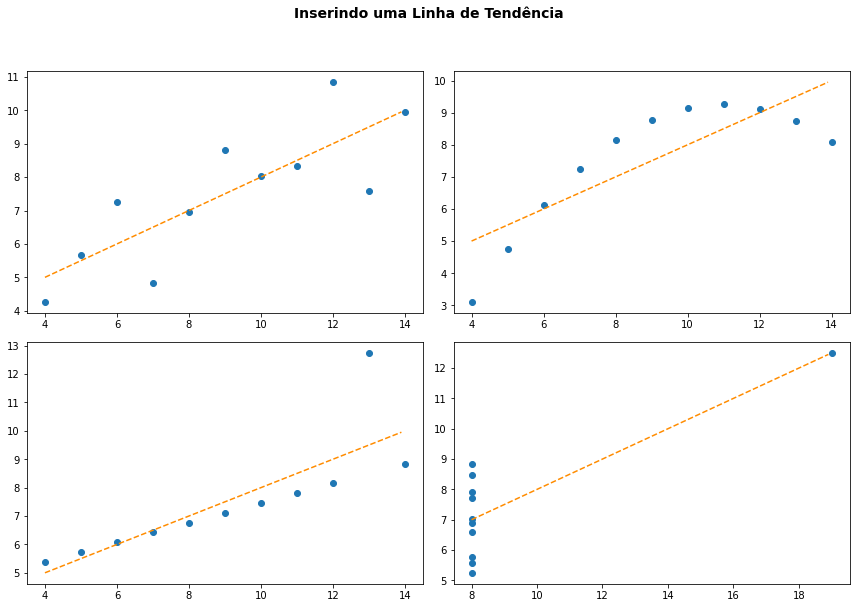
E podemos empregar a função também para aproximação com polinômios de grau maior.
fig, ax = plt.subplots(2,2,figsize=(12,8))
fig.suptitle('Inserindo uma Linha de Tendência', fontsize=14, weight='bold', y=1.05)
i = 0
for ds_type in df.dataset.unique():
ds = df[df.dataset == ds_type]
z = np.polyfit(ds.x, ds.y, 2)
p = np.poly1d(z)
ax[i//2,i%2].scatter(ds.x,ds.y)
x = np.arange(ds.x.min(), ds.x.max(), 0.1)
ax[i//2,i%2].plot(x,p(x),color='darkorange', linestyle='dashed')
i += 1
plt.tight_layout()
plt.show()
c:\users\user\anaconda3\lib\site-packages\IPython\core\interactiveshell.py:3418: RankWarning: Polyfit may be poorly conditioned
exec(code_obj, self.user_global_ns, self.user_ns)
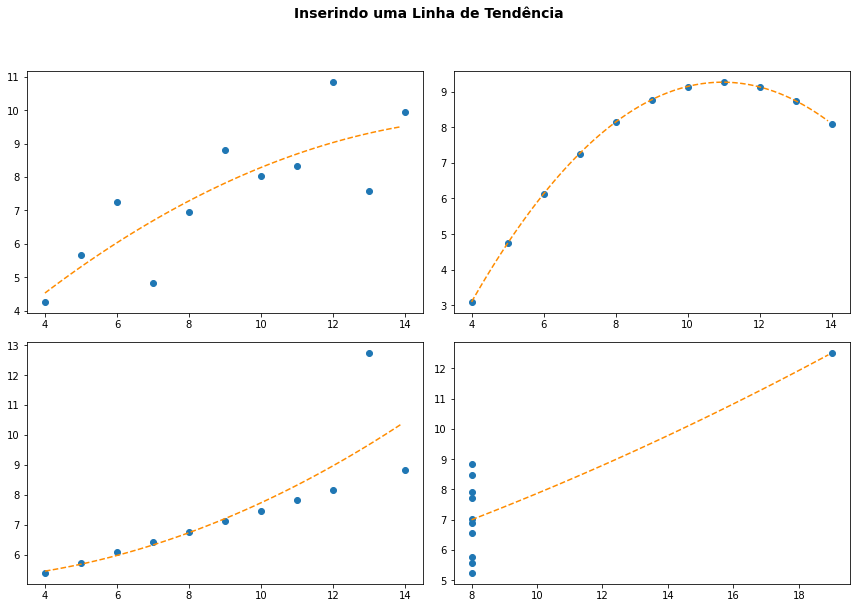
A vantagem desse método está em você poder empregar quaisquer outros otimizadores e fazer a aproximação com funções arbitrárias de sua escolha, não ficando assim restrito aos modelos linear ou polinomial.
O pacote SciPy é um eco-sistema Python para computação científica que inclui, dentre outros o NumPy e o Matplotlib. Ele fornece um método curve_fit() para obter os coeficientes que melhor aproximam um conjunto de pontos a uma função arbitrária de sua escolha. Os parâmetros obtidos da função são retornados em *popt e podem ser empregados para aplicar a função a um intervalo de valores que você deseja empregar do mesmo modo que no exemplo anterior.
from scipy.optimize import curve_fit
def func(x, a, b, c):
return a*np.sin(x) + b*np.cos(x) + x**c
fig, ax = plt.subplots(2,2,figsize=(12,8))
fig.suptitle('Inserindo uma Linha de Tendência', fontsize=14, weight='bold', y=1.05)
i = 0
for ds_type in df.dataset.unique():
ds = df[df.dataset == ds_type]
popt, pcov = curve_fit(func, ds.x, ds.y)
ax[i//2,i%2].scatter(ds.x,ds.y)
x = np.arange(ds.x.min(), ds.x.max(), 0.1)
ax[i//2,i%2].plot(x,func(x,*popt),color='darkorange', linestyle='dashed')
i += 1
plt.tight_layout()
plt.show()
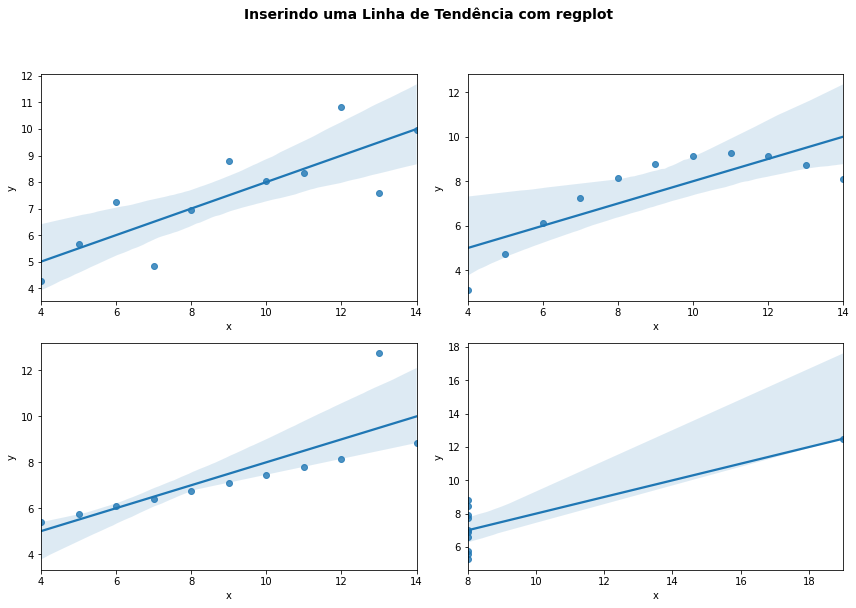
Mas se para você for suficiente empregar um modelo linear e apenas buscar essa tendência nos dados, você pode também querer empregar a função do pacote Seaborn, regplot(). Essa função exibe a linha de tendência linear dos dados adicionando ainda o intervalo de confiança dos dados com o modelo obtido.
O uso é também bastante simples,
sns.regplot(x='x', y='y', data=df)
e o comando acima irá exibir os pontos 'x' e 'y' de um DataFrame df com a linha de regressão linear e o intervalo de confiança correspondente.
fig, ax = plt.subplots(2,2,figsize=(12,8))
fig.suptitle('Inserindo uma Linha de Tendência com regplot', fontsize=14, weight='bold', y=1.05)
i = 0
for ds_type in df.dataset.unique():
ds = df[df.dataset == ds_type]
sns.regplot(x='x', y='y', data=ds, ax=ax[i//2,i%2])
i += 1
plt.tight_layout()
plt.show()
Você ainda pode pesquisar na documentação do Seaborn o gráfico sns.lmplot() que combina as funções regplot() e FacetGrid, uma classe que ajuda a combinar gráficos de diferentes subconjuntos de dados em vários painéis. Esse é um recurso específico do Seaborn e que não iremos explorar aqui, mas você pode experimentar o comando:
import seaborn as sns
sns.lmplot(x='x', y='y', col='dataset', data=df, scatter_kws={"s": 50, "alpha": 1})
plt.show()
Para exibir as linhas de tendência para os diferentes subconjuntos de dados tendo como filtro os diferentes valores do atributo dataset.
4.5.2. Linhas de Tendência no Modelo de uma Turbina Eólica¶
Vamos agora aplicar essas linhas de tendência ao nosso conjunto de dados de uma Turbina Eólica.
Reduzindo os dados ao intervalo de valores antes do patamar de saturação, podemos produzir as linhas de tendência linear e com um polinômio de grau 3.
data_T_AA = pd.read_csv('https://raw.githubusercontent.com/Rogerio-mack/Visualizacao-de-Dados-em-Python/main/data/T1_reshape.csv')
data_T_AA_mean = pd.read_csv('https://raw.githubusercontent.com/Rogerio-mack/Visualizacao-de-Dados-em-Python/main/data/T1_reshape_mean.csv')
data_T_AA.head()
| WindSpeed(m/s) | ActivePower(kW) | Theoretical_Power_Curve (KWh) | Loss_Value(kW) | Loss(%) | count | direction | |
|---|---|---|---|---|---|---|---|
| 0 | 3.5 | 43.46 | 70.58 | 27.12 | 38.02 | 29 | N |
| 1 | 4.0 | 88.01 | 127.57 | 39.56 | 31.60 | 101 | N |
| 2 | 4.5 | 160.51 | 217.01 | 56.50 | 26.42 | 102 | N |
| 3 | 5.0 | 274.71 | 335.67 | 60.96 | 18.44 | 99 | N |
| 4 | 5.5 | 388.60 | 465.84 | 77.24 | 16.79 | 119 | N |
data_T_AA_mean.head()
| WindSpeed(m/s) | ActivePower(kW) | Theoretical_Power_Curve (KWh) | Loss_Value(kW) | Loss(%) | count | |
|---|---|---|---|---|---|---|
| 0 | 3.5 | 52.191667 | 68.939167 | 16.745833 | 23.584167 | 56.250000 |
| 1 | 4.0 | 97.756667 | 127.686667 | 29.929167 | 23.646667 | 144.666667 |
| 2 | 4.5 | 183.601667 | 221.930000 | 38.327500 | 17.488333 | 149.500000 |
| 3 | 5.0 | 286.590833 | 336.426667 | 49.835000 | 14.937500 | 143.750000 |
| 4 | 5.5 | 400.392500 | 470.090833 | 69.699167 | 14.838333 | 167.666667 |
data_T_AA = data_T_AA[ data_T_AA["WindSpeed(m/s)"] < 12.5 ]
data_T_AA_mean = data_T_AA_mean[ data_T_AA_mean["WindSpeed(m/s)"] < 12.5 ]
fig, ax = plt.subplots(1,2,figsize=(12,6),sharey=True)
fig.suptitle('Modelo e dados reais de uma Turbina Eólica', fontsize=14, weight='bold', y=1.05)
ax[0].plot(data_T_AA_mean["WindSpeed(m/s)"],data_T_AA_mean["Theoretical_Power_Curve (KWh)"], '--k', label='Theorical', alpha=0.5)
ax[0].scatter(data_T_AA["WindSpeed(m/s)"],data_T_AA["ActivePower(kW)"], label='Real', marker='o', color='orange', alpha=0.5)
ax[1].plot(data_T_AA_mean["WindSpeed(m/s)"],data_T_AA_mean["Theoretical_Power_Curve (KWh)"], '--k', label='Theorical', alpha=0.5)
ax[1].scatter(data_T_AA["WindSpeed(m/s)"],data_T_AA["ActivePower(kW)"], label='Real', marker='o', color='orange', alpha=0.5)
x = np.arange(data_T_AA["WindSpeed(m/s)"].min(),data_T_AA["WindSpeed(m/s)"].max(), 0.1)
z = np.polyfit(data_T_AA["WindSpeed(m/s)"],data_T_AA["ActivePower(kW)"], 1)
p = np.poly1d(z)
ax[0].plot(x,p(x), linestyle='dashed', label='Linear(x)',linewidth=2, color='k')
z = np.polyfit(data_T_AA["WindSpeed(m/s)"],data_T_AA["ActivePower(kW)"], 3)
p = np.poly1d(z)
ax[1].plot(x,p(x), linestyle='dashed', label='P3(x)' ,linewidth=2, color='k')
ax[0].set_title("Curva de Energia Teória (KWh)", fontsize=14, weight='bold')
ax[1].set_title("Energia Real - Várias Turbinas (KWh)", fontsize=14, weight='bold')
ax[0].set_ylabel("Power (KWh)")
ax[0].set_xlabel("WindSpeed(m/s)")
ax[1].set_xlabel("WindSpeed(m/s)")
ax[0].legend(loc='lower right',fontsize=12)
ax[1].legend(loc='lower right',fontsize=12)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.tight_layout()
plt.show()
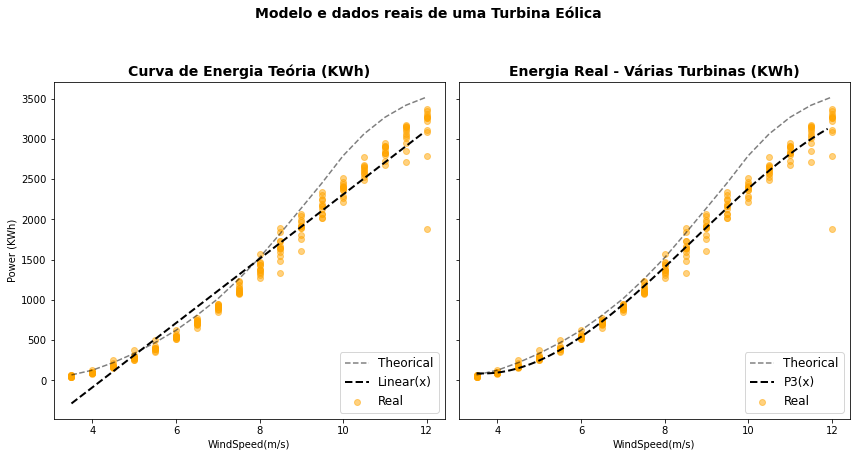
Como você pode ver o ajuste linear oferece pouca aderência aos dados coletados. Já modelo polinomial de grau 3, no intervalo de valores empregado, parece se ajustar até melhor que o próprio modelo teórico do fabricante!
4.5.3. Tendências e Séries Temporais¶
Na maior parte dos casos não vamos encontrar um modelo tão próximo como no exemplo anterior da nossa Turbina Eólica, mas interessa-nos apenas buscar definir melhor uma tendência de crescimento ou não dos valores. Nesses casos parece suficiente adotarmos simplesmente uma linha de tendência linear. Vamos ilustrar isso empregando o conjunto de dados de cotações de índice da bolsa.
\(\bigstar \text{ }\) Aqui você vai encontrar um problema muito comum ao buscarmos tendências em dados temporais. Sua variável independente (a linha do tempo) não pode ser aplicada diretamente a uma regressão linear (ou outra qualquer) pois seus dados não são numéricos. Para fazer isso teremos de empregar um artifício e transformar a linha do tempo em um atributo numérico.
Isso pode ser feito atribuindo-se para cada data do conjunto de dados um valor inteiro diferente a partir de 0. Se cada linha do conjunto de dados corresponde a uma data esse valor pode ser o próprio índice do seu conjunto de dados (para um DataFrame, df.index).
bovespa = pd.read_csv('https://raw.githubusercontent.com/Rogerio-mack/Visualizacao-de-Dados-em-Python/main/data/mystocksn.csv')
bovespa.data = pd.to_datetime(bovespa.data, format='%Y-%m-%d',errors='coerce') # somente para ajustar formato da datas
bovespa.head()
| data | IBOV | VALE3 | PETR4 | DOLAR | |
|---|---|---|---|---|---|
| 0 | 2020-02-27 | 102984.0 | 9.92 | 12.08 | 4.4491 |
| 1 | 2020-02-28 | 104172.0 | 9.82 | 12.10 | 4.4848 |
| 2 | 2020-03-02 | 106625.0 | 10.27 | 12.49 | 4.4413 |
| 3 | 2020-03-03 | 105537.0 | 10.22 | 12.16 | 4.4724 |
| 4 | 2020-03-04 | 107224.0 | 10.56 | 12.33 | 4.5132 |
bovespa.index
RangeIndex(start=0, stop=185, step=1)
fig, ax = plt.subplots(figsize=(14,6))
ax.plot(bovespa.data, bovespa.DOLAR, label='DOLAR')
ax.set_title('Tendência do Dólar (Regressão a Intervalo Fixo)', fontsize=14, weight='bold')
ax.set_xlabel("date")
ax.set_ylabel("Valor (R$)")
z = np.polyfit(bovespa.index,bovespa.DOLAR, 1)
p = np.poly1d(z)
ax.plot(bovespa.data,p(bovespa.index), linestyle='dashed', label='Linear(x)' ,linewidth=2, color='k')
# OU
# x = np.arange(0,len(bovespa),1)
# z = np.polyfit(x,bovespa.DOLAR, 1)
# p = np.poly1d(z)
# ax.plot(bovespa.data,p(x), linestyle='dashed', label='Linear(x)' ,linewidth=2, color='k')
ax.legend(fontsize=12)
import matplotlib.ticker as ticker
ax.xaxis.set_major_locator(ticker.MaxNLocator(8))
plt.show()
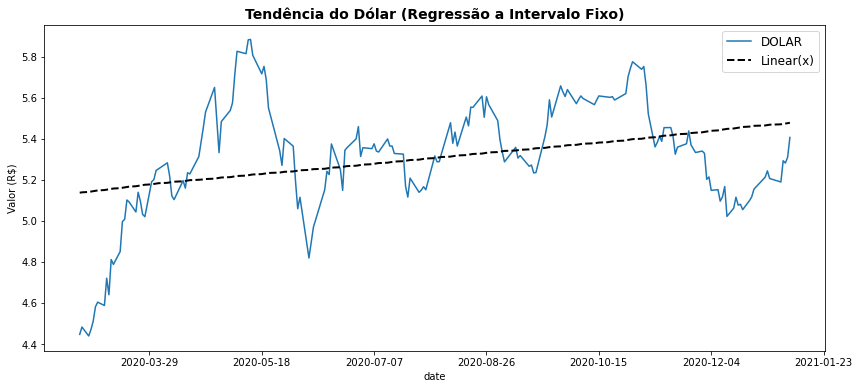
O procedimento acima será útil para você em muitos casos que envolvem séries temporais. Acima empregamos diretamente o índice dos dados (186 valores de \([0,185]\) para cada data) para linha de tempo da regressão mas, na ausência de um índice, poderíamos criar um valor diferente para cada data empregando:
x = np.arange(0,len(bovespa),1)
isso encontra-se comentado no código como uma forma opcional caso você precise desse procedimento.
Há entretanto uma série de detalhes quanto a isso. Por exemplo você pode ter intervalos de datas diferentes e, neste caso, pode ser necessário associar a cada data a distãncia em dias com relação a menor data do conjunto de dados e não valores com um incremento fixo como acima.
Mesmo no nosso exemplo, como os dados da bolsa referem-se somente a dias úteis há um intervalo de datas maior nos finais de semana e, embora os resultados sejam praticamente os mesmos aqui, a rigor precisáriamos empregar intervalos de data diferentes e para outros casos isso pode ser realmente necessário. Fazemos esse procedimento abaixo incluindo uma variável que corresponde a quantidade de dias a partir da data inicial e a função dt.days permite transformar esses valores em numéricos para o cálculo da regressão.
bovespa['dias'] = bovespa['data'] - bovespa['data'].min()
fig, ax = plt.subplots(figsize=(14,6))
ax.plot(bovespa.data, bovespa.DOLAR, label='DOLAR')
ax.set_title('Tendência do Dólar (Regressão a Intervalo Variável)', fontsize=14, weight='bold')
ax.set_xlabel("date")
ax.set_ylabel("Valor (R$)")
z = np.polyfit(bovespa.dias.dt.days,bovespa.DOLAR, 1)
p = np.poly1d(z)
ax.plot(bovespa.data,p(bovespa.dias.dt.days), linestyle='dashed', label='Linear(x)' ,linewidth=2, color='k')
ax.legend(fontsize=12)
import matplotlib.ticker as ticker
ax.xaxis.set_major_locator(ticker.MaxNLocator(8))
plt.show()
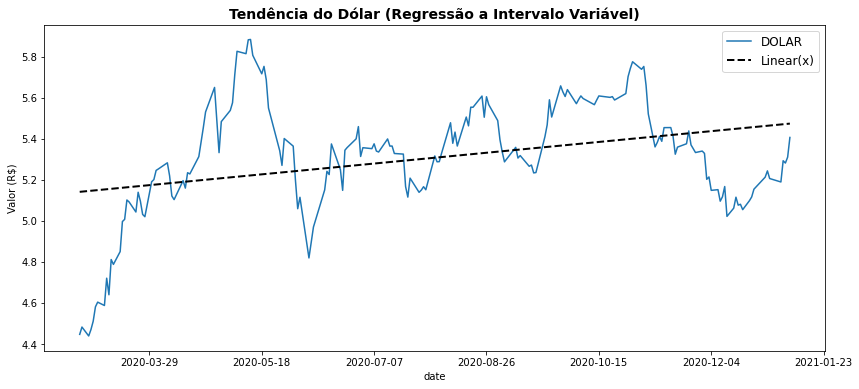
Aqui o resultado é praticamente o mesmo, mas para os casos onde os intervalos de data tenham uma proporções maiores com relação ao início e fim do intervalo, ou muitos ‘buracos’ de datas, isso pode ser relevante.
4.5.4. Linha de Tendência com Média dos Dados¶
Uma outra forma de entendermos as linhas de tendência dos dados é empregarmos a média dos vários valores e ligar esses pontos a uma linha de tendência. Aqui não buscamos aproximar nenhum modelo, como um modelo linear ou polinomial, mas simplesmente exibir uma média de tendência dos dados.
fig, ax = plt.subplots(figsize=(14,6))
data_T_AA = pd.read_csv('https://raw.githubusercontent.com/Rogerio-mack/Visualizacao-de-Dados-em-Python/main/data/T1_reshape.csv')
data_T_AA_mean = pd.read_csv('https://raw.githubusercontent.com/Rogerio-mack/Visualizacao-de-Dados-em-Python/main/data/T1_reshape_mean.csv')
plt.plot(data_T_AA_mean["WindSpeed(m/s)"],data_T_AA_mean["Theoretical_Power_Curve (KWh)"],'--k',label='Theorical')
plt.plot(data_T_AA_mean["WindSpeed(m/s)"],data_T_AA_mean["ActivePower(kW)"], marker='o', color='r', linewidth=1, label='Trend')
plt.scatter(data_T_AA["WindSpeed(m/s)"],data_T_AA["ActivePower(kW)"], marker='o', color='orange', alpha=0.7, s=64, label='Samples')
plt.title("Energia Real - Várias Turbinas (KWh)", fontsize=14, weight='bold')
plt.ylabel("Power (KWh)")
plt.xlabel("WindSpeed(m/s)")
plt.legend()
plt.show()
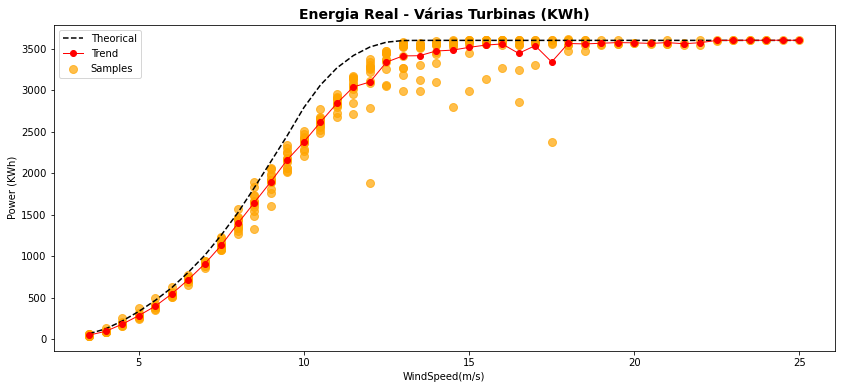
Essa linha média ainda pode ser incrementada com uma margem de erro, por exemplo o desvio padrão, permitindo acompanhar a dispersão dos dados ao longo da linha média. Para isso, no lugar do plot você pode empregar o comando plt.errorbar.
Vamos empregar isso em nosso conjunto de dados da bolsa de valores. Como nossos dados apresentam apenas uma única cotação diária, vamos agregar a cotações e exibir as cotações mensais ao longo dos doze meses da base.
bovespa['mes'] = bovespa['data'].dt.month
bovespa['mes'] = bovespa['mes'] - 1
bovespa.at[ bovespa['mes'] == 0 , 'mes' ] = 12
bovespa.head()
| data | IBOV | VALE3 | PETR4 | DOLAR | dias | mes | |
|---|---|---|---|---|---|---|---|
| 0 | 2020-02-27 | 102984.0 | 9.92 | 12.08 | 4.4491 | 0 days | 1 |
| 1 | 2020-02-28 | 104172.0 | 9.82 | 12.10 | 4.4848 | 1 days | 1 |
| 2 | 2020-03-02 | 106625.0 | 10.27 | 12.49 | 4.4413 | 4 days | 2 |
| 3 | 2020-03-03 | 105537.0 | 10.22 | 12.16 | 4.4724 | 5 days | 2 |
| 4 | 2020-03-04 | 107224.0 | 10.56 | 12.33 | 4.5132 | 6 days | 2 |
fig, ax = plt.subplots(figsize=(14,6))
yerr = []
ymean = []
for mes in bovespa.mes.unique():
yerr.append(bovespa[bovespa.mes == mes]['IBOV'].std())
ymean.append(bovespa[bovespa.mes == mes]['IBOV'].mean())
yerr = np.array(yerr)
ymean = np.array(ymean)
plt.errorbar(bovespa.mes.unique(), ymean, yerr=yerr, label='Tendência', marker='o', color='r', linewidth=1.2)
plt.scatter(bovespa.mes, bovespa.IBOV, label='Valores Mês', marker='o', color='orange', alpha=0.7, s=64)
plt.title("Tendência do Índice Bovespa", fontsize=14, weight='bold')
plt.xlabel("Mês")
plt.ylabel("Pontos")
plt.legend()
plt.show()
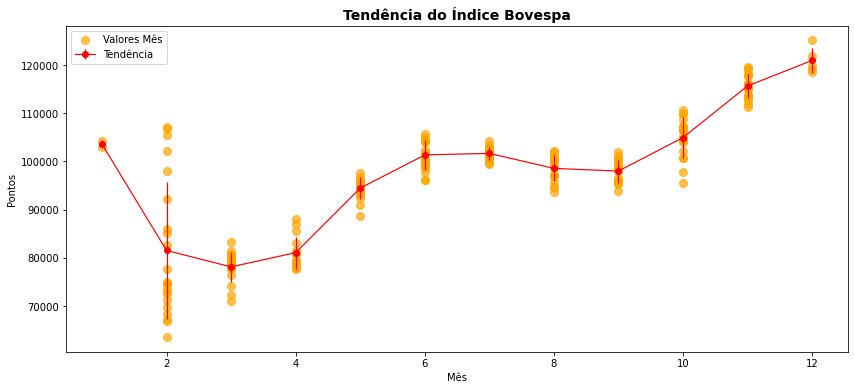
O mesmo procedimento poderia ser feito se tivéssemos cotações diárias do índice e se já você acompanhou gráficos empregados na análise técnica de ações da bolsa na mídia ou em aplicativos de investimento, deve notar semelhança dos gráficos. No caso de ações da bolsa, entretanto, é mais comum essa tendência ser acompanhada de gráfico de caixa, ou boxplot como abaixo.
fig, ax = plt.subplots(figsize=(14,6))
plt.plot(bovespa.mes.unique(), ymean, label='Tendência', marker='o', color='b', linewidth=1.2, markersize=4)
plt.scatter(bovespa.mes, bovespa.IBOV, label='Valores Mês', marker='o', color='orange', alpha=0.4, s=64)
for mes in bovespa.mes.unique():
plt.boxplot(bovespa[bovespa.mes == mes].IBOV, positions=[mes], widths=0.15, flierprops=dict(color='r',markeredgecolor='r'),medianprops=dict(color='k'))
plt.title("Tendência do Índice Bovespa", fontsize=14, weight='bold')
plt.xlabel("Mês")
plt.ylabel("Pontos")
plt.legend()
plt.show()
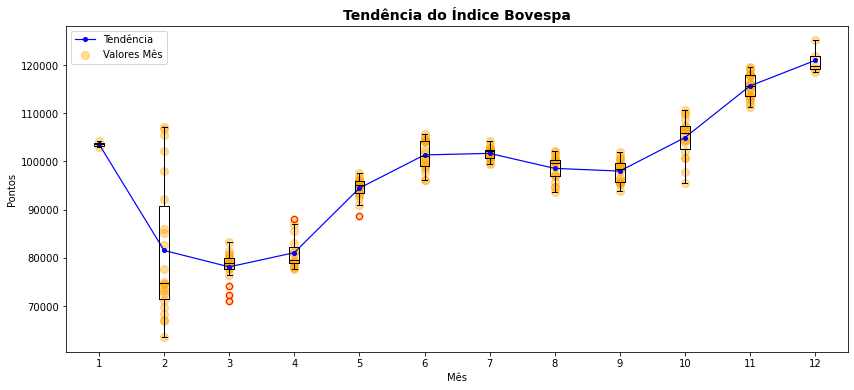
O gráficos de caixa foram introduzidos nos anos 70 por John Tukey como uma forma sintética de exibir a distribuição dos dados e vem sendo largamente empregados desde então. Esse e outros gráficos de distribuição é o que estudaremos a seguir no capítulo de Distribuição.
4.6. Trabalhando com Escalas Diferentes¶
Se você empregar agora diretamente o gráfico anterior para analisar a tendência não só do dólar mas também do índice Bovespa o resultado não irá parecer dos melhores.
fig, ax = plt.subplots(figsize=(14,6))
ax.plot(bovespa.data, bovespa.DOLAR, label='DOLAR')
ax.plot(bovespa.data, bovespa.IBOV, label='IBOVESPA')
ax.set_title('Tendência do Dólar e IBOVESPA', fontsize=14, weight='bold')
ax.set_xlabel("date")
ax.set_ylabel("Valor (R$) / Pontos")
z = np.polyfit(bovespa.dias.dt.days,bovespa.DOLAR, 1)
p = np.poly1d(z)
ax.plot(bovespa.data,p(bovespa.dias.dt.days), linestyle='dashed', label='Linear DOLAR' ,linewidth=2, color='k')
z = np.polyfit(bovespa.dias.dt.days,bovespa.IBOV, 1)
p = np.poly1d(z)
ax.plot(bovespa.data,p(bovespa.dias.dt.days), linestyle='dashed', label='Linear IBOV' ,linewidth=2, color='r')
ax.legend(fontsize=12)
import matplotlib.ticker as ticker
ax.xaxis.set_major_locator(ticker.MaxNLocator(8))
plt.show()
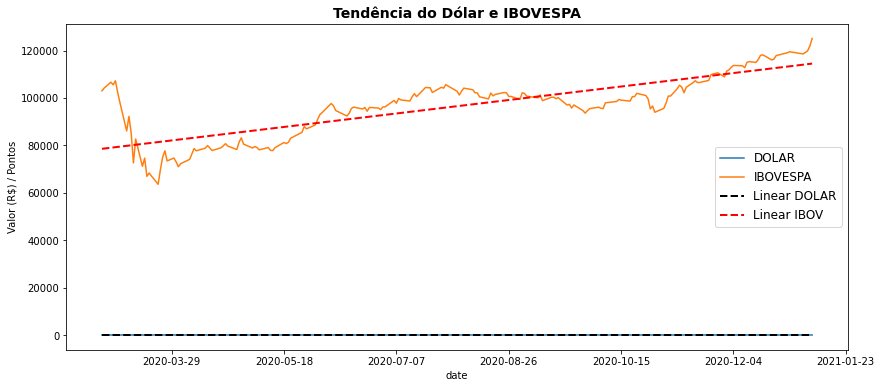
Se você observou com atenção o mal resultado dessa visualização é por que os dados estão em escalas de valores muito diferentes e você não consegue, no mesmo gráfico, observar claramente as variáveis do dólar que encontram-se em um intervalo \(4 \pm 1\) de valores e os valores de índice Bovespa, no intervalo \(100000 \pm 10000\).
O comando ax.twinx() no modo Artist Layer pode ser uma alternativa. Ele permite apresentar duas escalas diferentes no mesmo gráfico e podemos assim comparar a tendência das duas séries de dados simultaneamente.
fig, ax = plt.subplots(figsize=(14,6))
ax.plot(bovespa.data, bovespa.DOLAR, label='DOLAR', color='k', alpha=0.3)
ax2 = ax.twinx() # instantiate a second axes that shares the same x-axis
ax2.plot(bovespa.data, bovespa.IBOV, label='IBOVESPA', color='r', alpha=0.3)
ax.set_title('Tendência do Dólar e IBOVESPA', fontsize=14, weight='bold')
ax.set_xlabel("date")
ax.set_ylabel("Valor (R$)")
ax2.set_ylabel("Pontos")
z = np.polyfit(bovespa.dias.dt.days,bovespa.DOLAR, 1)
p = np.poly1d(z)
ax.plot(bovespa.data,p(bovespa.dias.dt.days), linestyle='dashed', label='Linear DOLAR' ,linewidth=2, color='k')
z = np.polyfit(bovespa.dias.dt.days,bovespa.IBOV, 1)
p = np.poly1d(z)
ax2.plot(bovespa.data,p(bovespa.dias.dt.days), linestyle='dashed', label='Linear IBOV' ,linewidth=2, color='r')
ax.legend(loc='lower right',fontsize=12)
ax2.legend(fontsize=12)
import matplotlib.ticker as ticker
ax.xaxis.set_major_locator(ticker.MaxNLocator(8))
plt.show()
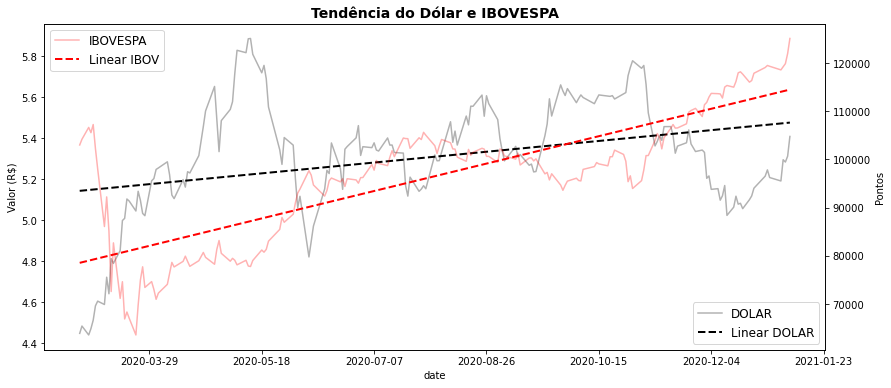
Esse procedimento, entretanto, só é útil quando temos até duas escalas diferentes de dados. Para mais de duas escalas a forma que podemos empregar é a normalização dos dados.
\(\bigstar \text{ }\) Cuidado ao empregar normalizações dos dados! Ao exibir os dados normalizados você não estará mais observando os valores reais dos dados, mas apenas seus movimentos relativos.
Existem várias formas de normalização e poderíamos aqui aplicar simplesmente uma normalização min/max dividindo cada valor pelo seu valor máximo levando, assim, cada atributo para valores entre \([0,1]\). Mas vamos adotar um procedimento muito usado, e igualmente simples, e aplicar uma normalização normalmente conhecida como standard scaler que normaliza os valores a uma média 0 e desvio padrão 1.
O resultado encontra-se abaixo.
bovespa_norm = ( bovespa.drop(columns=['data','dias']) - bovespa.drop(columns=['data','dias']).mean() ) / bovespa.drop(columns=['data','dias']).std()
bovespa_norm = pd.concat([bovespa[['data','dias']], bovespa_norm],axis=1)
bovespa_norm.head()
| data | dias | IBOV | VALE3 | PETR4 | DOLAR | mes | |
|---|---|---|---|---|---|---|---|
| 0 | 2020-02-27 | 0 days | 0.488931 | -0.464186 | 2.132811 | -3.018888 | -1.797812 |
| 1 | 2020-02-28 | 1 days | 0.578304 | -0.500953 | 2.144005 | -2.893685 | -1.797812 |
| 2 | 2020-03-02 | 4 days | 0.762844 | -0.335505 | 2.362293 | -3.046244 | -1.475842 |
| 3 | 2020-03-03 | 5 days | 0.680993 | -0.353888 | 2.177588 | -2.937172 | -1.475842 |
| 4 | 2020-03-04 | 6 days | 0.807907 | -0.228884 | 2.272739 | -2.794083 | -1.475842 |
fig, ax = plt.subplots(figsize=(14,6))
ax.plot(bovespa_norm.data, bovespa_norm.VALE3, label='VALE3', alpha=0.5)
ax.plot(bovespa_norm.data, bovespa_norm.PETR4, label='PETR4', alpha=0.5)
ax.plot(bovespa_norm.data, bovespa_norm.DOLAR, label='DOLAR', alpha=0.5)
ax.plot(bovespa_norm.data, bovespa_norm.IBOV, label='IBOV')
ax.set_title('Bolsa Ações', fontsize=14, weight='bold')
ax.set_xlabel("date")
ax.set_ylabel("Tendência dos Valores")
ax.legend(fontsize=12)
import matplotlib.ticker as ticker
ax.xaxis.set_major_locator(ticker.MaxNLocator(8))
plt.show()
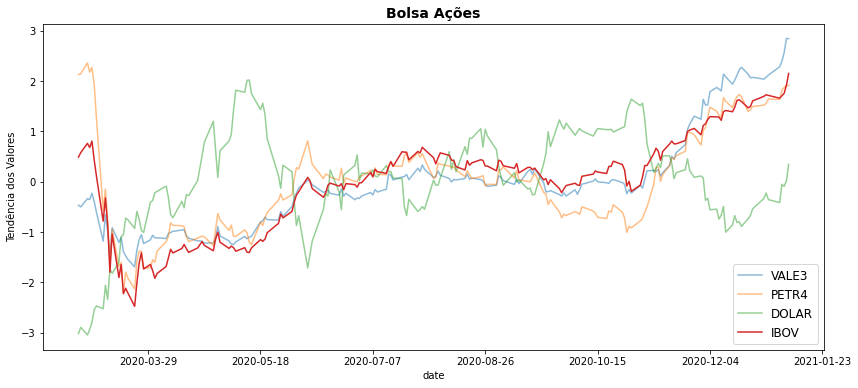
Não é nosso objetivo tirar conclusões sobre esses dados aqui. Nosso interesse é apenas nas técnicas de visualização e análise empregados. Mas você pode, por exemplo, observar que o índice da bolsa segue de forma bastante próxima os movimentos das ações da VALE3 e PETR4 e identificar a presença de vales do índice quando de fortes aumentos do dólar e podemos deixar a uma análise melhor desses movimentos para os economistas e analistas de mercado.
4.7. \(\bigstar \text{ }\) Um Cuidado no Uso do plt.plot()¶
Esse é um erro tão comum no uso do plt.plot() que vale a pena voltarmos nele aqui antes de prosseguirmos para o próximo capítulo. Evite produzir gráficos de linha com o Matplotlib quando há mais de ponto para a mesma coordenada. Se você já entendeu isso pode saltar esta seção, mas vamos entender melhor o que isso significa.
import seaborn as sns
fig, ax = plt.subplots(figsize=(12,8),sharex=True,sharey=True)
plt.subplot(2,2,1)
plt.plot(bovespa.mes, bovespa.IBOV, label='Valores Mês', color='r')
plt.title("ERRADO", fontsize=14, weight='bold', color='r')
plt.xlabel("Mês")
plt.ylabel("Pontos")
plt.legend()
plt.subplot(2,2,2)
plt.scatter(bovespa.mes, bovespa.IBOV, label='Valores Mês', marker='o', color='b', alpha=0.1, s=64)
plt.plot(bovespa.mes, bovespa.IBOV, label='Vários Valores', color='r')
plt.title("ERRADO", fontsize=14, weight='bold', color='r')
plt.xlabel("Mês")
plt.ylabel("Pontos")
plt.legend()
plt.subplot(2,2,3)
plt.plot(bovespa.mes.unique(), ymean, label='Média dos Valores', marker='o', color='b', linewidth=1.2, markersize=4)
plt.scatter(bovespa.mes, bovespa.IBOV, label='Valores Mês', marker='o', color='b', alpha=0.1, s=64)
plt.title("CORRETO", fontsize=14, weight='bold', color='b')
plt.xlabel("Mês")
plt.ylabel("Pontos")
plt.legend()
plt.subplot(2,2,4)
sns.lineplot(x=bovespa.mes, y=bovespa.IBOV, label='Valores Mês', alpha=0.4)
plt.title("CORRETO", fontsize=14, weight='bold', color='b')
plt.xlabel("Mês")
plt.ylabel("Pontos")
plt.legend()
plt.tight_layout()
plt.show()
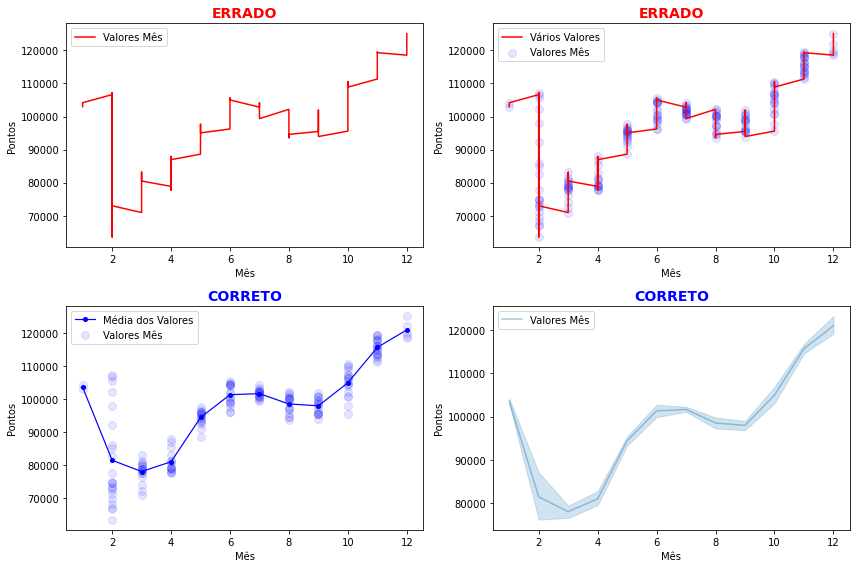
O gráfico plt.plot do Matplotlib conecta cada ponto de dados por uma linha. Portanto, havendo mais de um ponto de dados para uma mesma coordenada o resultado é o que você pode encontrar no primeiro gráfico da figura acima o que, certamente não é o que você desejaria para representar os dados. O erro fica claramente exibido no gráfico seguinte que mostra os vários pontos de dados de uma mesma coordenada ligados.
Nesses casos é mais adequado empregar um scatter plot e, se quiser adicionar uma linha média como fizemos nos exemplos anteriores ou aqui no terceiro gráfico. O sns.lineplot do pacote Seaborn também pode ser uma opção já tem um comportamento diferente do plt.plot. Ele já exibe por padrão a linha média dos dados e adiciona um intervalo de confiança em torno desses valores. Quaisquer dessas opções são corretas e podem ser então empregadas.
Obviamente não é nosso propósito fazer uma análise completa e conclusiva desses dados aqui, mas podemos ter uma ideia das relações entre buscas de termos no Google, a evolução de casos de Covid e seus impactos na Bolsa, e você pode observar aqui o potencial de empregarmos a visualização de dados para entender a evolução desses dados. Vamos então ver alguns instrumentos úteis para melhor a investigação de dados como esses a partir de gráficos de linha. O primeiro trata de como adicionarmos linhas de tendência e segundo sobre dados que apresentam se apresentam em diferentes escalas.
